揭秘圆柱体表面积的计算方法
圆柱体表面积是几何学中一个重要的概念,它涉及到圆柱体的外部覆盖面积。圆柱体是一个具有两个平行且相等的圆形底面以及一个侧面连接这两个底面的立体图形。为了深入理解圆柱体表面积的计算方法,我们需要从圆柱体的基本组成开始探讨。
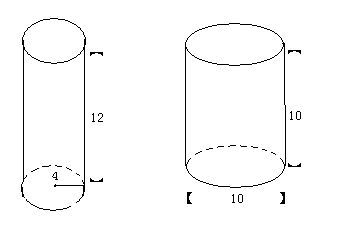
圆柱体的表面积主要由两部分组成:底面积和侧面积。底面积是圆柱体两个圆形底面的面积总和,而侧面积是圆柱体侧面展开后的矩形面积。在圆柱体中,我们通常将底面的半径记作r,将圆柱体的高记作h。
首先,我们来看圆柱体的底面积。圆柱体有两个底面,每个底面都是一个圆。圆的面积计算公式是π乘以半径的平方,即πr²。因此,两个底面的总面积就是2πr²。这里的π是一个数学常数,约等于3.14159。
接下来,我们分析圆柱体的侧面积。圆柱体的侧面是一个曲面,当我们将这个曲面展开时,它会变成一个矩形。这个矩形的长等于圆柱体底面的周长,而矩形的宽等于圆柱体的高。圆的周长计算公式是2π乘以半径,即2πr。因此,展开后的矩形的长就是2πr,而宽就是h。矩形的面积计算公式是长乘以宽,所以圆柱体的侧面积就是2πr乘以h,即2πrh。
现在,我们已经知道了圆柱体的底面积和侧面积的计算方法,那么圆柱体的总表面积就是将这两者相加。因此,圆柱体的表面积计算公式就是底面积加侧面积,即2πr²加2πrh。这个公式可以帮助我们快速准确地计算出任何给定半径和高度的圆柱体的表面积。
圆柱体表面积的概念不仅在几何学中有重要意义,还在许多实际应用中发挥着关键作用。例如,在包装、建筑、工程等领域,我们经常需要计算圆柱体的表面积来确定所需的材料数量。在包装设计中,了解圆柱体的表面积可以帮助我们确保包装材料能够完全覆盖产品,同时避免浪费。在建筑和工程中,计算圆柱体的表面积对于确定建筑材料的使用量和成本至关重要。
此外,圆柱体表面积的计算还涉及到一些有趣的数学问题。例如,如何找到给定表面积下圆柱体的最大体积?这是一个典型的优化问题,可以通过微积分等数学工具来解决。这类问题不仅在数学研究中具有理论价值,还在工程设计和生产实践中具有实际应用价值。
在计算圆柱体表面积时,我们还需要注意一些常见的误区。例如,有些人可能会忽略圆柱体的两个底面,只计算侧面积;或者有些人可能会错误地将圆柱体的侧面展开成一个正方形而不是矩形。这些错误都会导致计算结果的偏差。因此,在计算圆柱体表面积时,我们需要仔细核对公式和步骤,确保计算结果的准确性。
除了基本的圆柱体表面积计算外,我们还可以探讨一些特殊情况下的圆柱体表面积。例如,当圆柱体的高度等于底面直径时,我们称这种圆柱体为等径圆柱体。等径圆柱体的表面积计算具有一些特殊性质,可以通过简化公式来快速求解。此外,我们还可以考虑圆柱体被切割或拼接后的表面积变化问题。这些问题虽然复杂一些,但通过运用几何知识和逻辑推理能力,我们仍然可以找到解决方案。
总的来说,圆柱体表面积是一个既基础又重要的几何概念。它不仅在数学学习中占据重要地位,还在许多实际应用中发挥着关键作用。通过深入理解和掌握圆柱体表面积的计算方法和性质,我们可以更好地解决相关数学问题,并应用到实际生活中去。同时,我们还可以不断拓展和深化对圆柱体表面积的研究和探索,发现更多有趣的数学问题和实际应用价值。
在实际应用中,我们还需要注意圆柱体表面积的精度和单位问题。在计算过程中,我们需要确保所使用的数据是准确的,并且单位是一致的。例如,在计算圆柱体的表面积时,我们需要确保半径和高度的单位是相同的(如都是米或都是厘米),这样才能得到正确的结果。此外,在精度要求较高的场合(如工程设计或科学研究),我们还需要考虑使用更精确的数值计算方法或工具来得到更准确的结果。
总之,圆柱体表面积是一个具有广泛应用价值的几何概念。通过深入理解和掌握其计算方法和性质,我们可以更好地解决相关数学问题,并将其应用到实际生活中去。同时,我们还需要不断学习和探索新的数学知识和方法,以应对日益复杂的数学问题和实际应用挑战。
- 上一篇: 田园犬欢乐瞬间集锦小视频
- 下一篇: 如何发布个人微博教程
-
 圆柱的侧面积计算公式及详解新闻资讯10-28
圆柱的侧面积计算公式及详解新闻资讯10-28 -
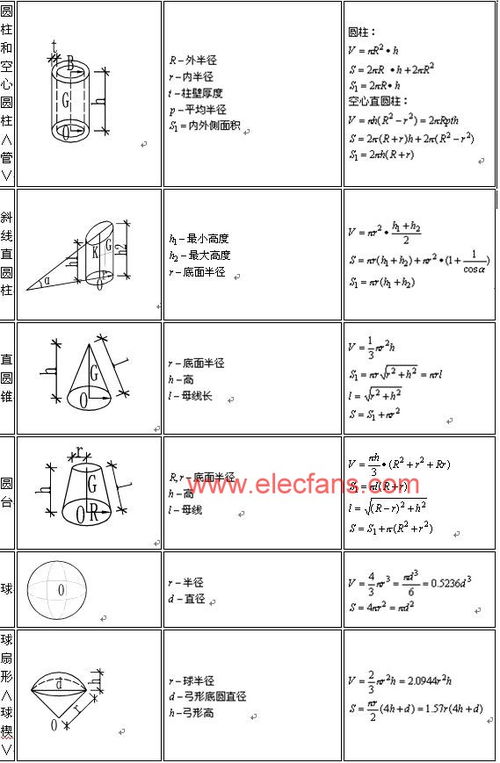 梯形体积该如何计算?新闻资讯11-12
梯形体积该如何计算?新闻资讯11-12 -
 圆柱体体积的计算方法新闻资讯11-13
圆柱体体积的计算方法新闻资讯11-13 -
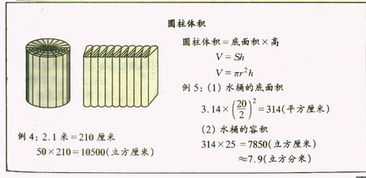 揭秘!圆柱体积计算的神奇公式,轻松掌握空间奥秘新闻资讯10-19
揭秘!圆柱体积计算的神奇公式,轻松掌握空间奥秘新闻资讯10-19 -
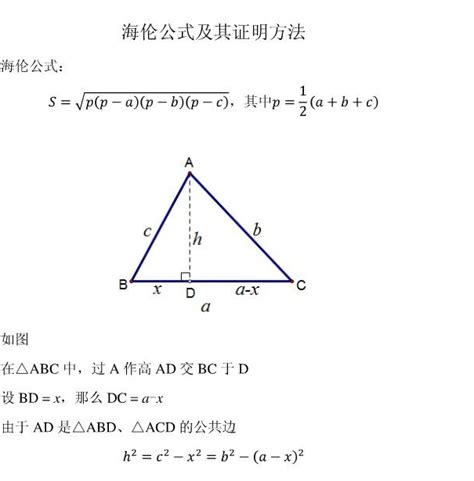 三角形面积计算方法大揭秘!新闻资讯11-25
三角形面积计算方法大揭秘!新闻资讯11-25 -
 揭秘!圆锥表面积的神奇计算公式,一看就懂!新闻资讯11-01
揭秘!圆锥表面积的神奇计算公式,一看就懂!新闻资讯11-01












