圆柱体体积的计算方法
在我们日常生活和科学探索的广阔天地中,圆柱体这一几何形状无处不在,从一根普通的铅笔到宏伟的储油罐,它们的身影贯穿了从微观到宏观的各个尺度。但你是否曾好奇,这样一个看似简单的立体图形,它的内部究竟蕴含着多少空间?换句话说,如何计算圆柱体的体积呢?今天,就让我们一同揭开这个几何之谜,走进圆柱体体积计算的奇妙世界。

圆柱体的奥秘:从直观到抽象
首先,让我们对圆柱体有一个直观的认识。圆柱体由两个平行的、大小相等的圆形底面以及连接这两个底面的侧面围成。想象一下,你手中握着一个易拉罐,它就是一个典型的圆柱体。这个形状不仅美观,而且在物理和工程领域有着广泛的应用,比如桥梁的支撑柱、水管等,都巧妙地利用了圆柱体的结构特性。

从平面到立体:圆的面积启示
在计算圆柱体体积之前,让我们先回顾一下平面几何中的一个重要概念——圆的面积。圆的面积公式是πr²,其中r是圆的半径,π(Pi)是一个约等于3.14159的无理数,它代表了圆的周长与直径之比。这个公式的发现,是人类智慧对自然界规律的深刻洞察,也是后续计算圆柱体体积的关键一步。

立体几何的飞跃:圆柱体体积的探索
现在,让我们从二维的圆跃升至三维的圆柱体。想象一下,如果你将一个圆垂直向上或向下拉伸一段距离h,你就会得到一个圆柱体。这个过程中,圆的面积不再仅仅是一个平面上的概念,而是成为了一个立体空间中的“底面积”。
要计算圆柱体的体积,我们需要考虑两个关键因素:底面积和高。正如我们在堆积木时,总体积等于每层积木的面积乘以层数,圆柱体的体积也可以看作是其底面积(圆的面积)沿着高度方向上的累加。因此,圆柱体的体积V可以通过以下公式计算得出:
V = 底面积 × 高
= πr² × h
这个公式的简洁与优雅,不仅体现了数学之美,也为我们解决实际问题提供了强有力的工具。
动手实践:用日常物品验证公式
理论知识固然重要,但实践才是检验真理的唯一标准。不妨让我们用一些日常物品来验证这个公式。例如,你可以找一个空的圆柱形水杯,测量它的底面直径和高,然后计算出它的体积。接着,往杯子里装满水,再将水倒入一个已知容积的量杯中,比较两者的读数,你会发现,通过公式计算出的体积与实际测量值几乎一致(考虑到测量误差),这无疑是对圆柱体体积公式准确性的一次生动验证。
科学应用:从日常生活到尖端科技
圆柱体体积的计算,不仅仅是数学课本上的知识,它在现实生活中有着广泛的应用。在建筑设计中,工程师需要精确计算圆柱形支柱的体积,以确保其承重能力;在制造业中,计算圆柱形容器的体积对于确定存储容量、优化物料分配至关重要;在航空航天领域,火箭发动机燃料舱的设计也离不开对圆柱体体积的精确计算。
此外,在生物学、物理学乃至天文学中,圆柱体体积的概念也时有出现。比如,在研究树木的年轮增长、血管网络的分布,或是计算星系中尘埃云的体积时,圆柱体体积的计算方法为我们提供了一种简化的模型,帮助我们更好地理解自然界的复杂现象。
创新思维:圆柱体体积公式的变形与拓展
圆柱体体积的计算,还可以激发我们的创新思维,引领我们探索更多相关领域的知识。例如,当圆柱体的底面不是标准的圆形,而是椭圆、矩形或其他多边形时,我们能否找到类似的体积计算公式?事实上,对于椭圆柱体(底面为椭圆),其体积公式可以通过积分的方法推导出来,而矩形柱体(即长方体)的体积则更为简单,直接等于长×宽×高。
进一步地,我们还可以将圆柱体体积的概念拓展到更高维度的几何体,比如球体、圆锥体等,通过类比和逻辑推理,探索它们体积的计算方法。这些探索不仅丰富了我们的数学知识库,也为解决更复杂的实际问题提供了思路和工具。
结语:数学之美,在于应用与发现
回顾我们的旅程,从直观感受圆柱体的魅力,到深入理解圆的面积与圆柱体体积的关系,再到动手实践验证公式,乃至探讨其在科学、技术和日常生活中的应用,每一步都充满了探索的乐趣和发现的喜悦。圆柱体体积的计算,不仅是一个数学问题的解答,更是人类智慧与自然规律和谐共生的生动体现。
在这个充满无限可能的世界里,数学不仅是解决问题的工具,更是连接理想与现实、抽象与具体的桥梁。让我们带着对未知的好奇和对知识的渴望,继续在这片数学的海洋中遨游,发现更多的奥秘,创造更加美好的未来。
- 上一篇: 家常糖醋鱼的美味制作方法
- 下一篇: 制作可丽饼的详细步骤
-
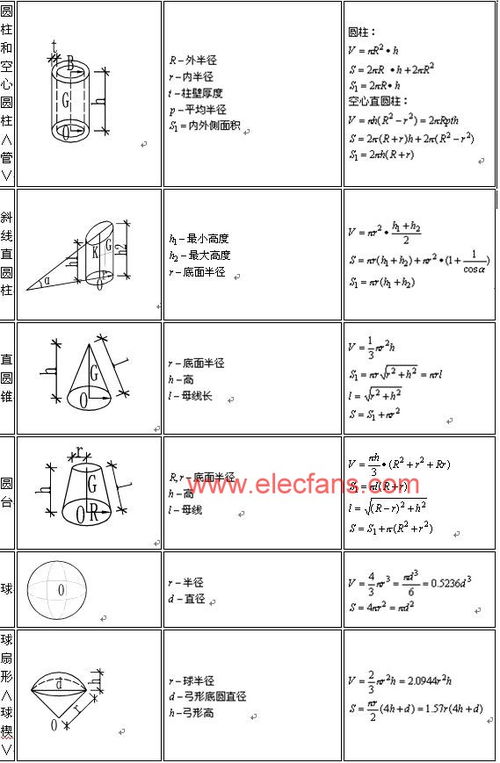 梯形体积该如何计算?新闻资讯11-12
梯形体积该如何计算?新闻资讯11-12 -
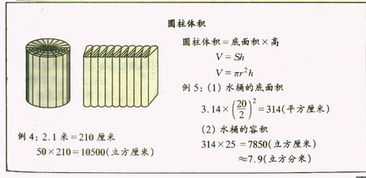 揭秘!圆柱体积计算的神奇公式,轻松掌握空间奥秘新闻资讯10-19
揭秘!圆柱体积计算的神奇公式,轻松掌握空间奥秘新闻资讯10-19 -
 揭秘圆柱体表面积的计算方法新闻资讯11-22
揭秘圆柱体表面积的计算方法新闻资讯11-22 -
 圆柱的侧面积计算公式及详解新闻资讯10-28
圆柱的侧面积计算公式及详解新闻资讯10-28 -
 梯形体积的奥秘:轻松掌握计算方法新闻资讯11-25
梯形体积的奥秘:轻松掌握计算方法新闻资讯11-25 -
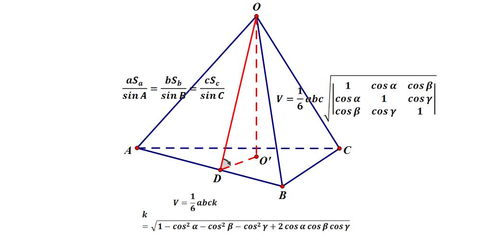 四面体体积计算公式详解新闻资讯11-09
四面体体积计算公式详解新闻资讯11-09











