揭秘!坐标轴上两点间距离的超简单计算公式
在探讨平面几何与坐标系统的交汇处,一个至关重要的概念便是“坐标轴上两点间距离公式”。这一公式不仅是连接代数与几何的桥梁,也是解决众多实际问题中距离测量问题的基石。本文旨在简明扼要地介绍这一公式的由来、形式、应用及其重要性,同时确保内容原创度高、结构清晰,并合理布局关键词,以提升读者体验与搜索引擎的友好性。

引言
在二维或三维空间中,确定任意两点之间的距离是数学与物理学、工程学等多个领域的基本需求。当这两点位于坐标轴上时,其距离的计算尤为直接且富有几何意义。坐标轴上的点,无论是横轴(X轴)还是纵轴(Y轴),其位置均由唯一的数值(坐标)确定,这使得两点间距离的计算变得相对简单而明确。
坐标轴上两点间距离公式的形式
一维坐标轴(如X轴或Y轴)
在一维坐标轴上,两点间的距离计算最为直观。假设有两点A和B,它们的坐标分别为$x_1$和$x_2$(若考虑Y轴,则坐标相应为$y_1$和$y_2$,但原理相同),则两点间的距离$d$可通过以下公式计算:
$$d = |x_2 - x_1|$$
或对于Y轴上的点:
$$d = |y_2 - y_1|$$
这里的绝对值符号“| |”表示距离总是非负的,即不考虑方向只考虑大小。
解释与应用
解释:该公式基于坐标轴上点之间的位置差异(即坐标之差),通过取绝对值确保结果为正数,直接给出了两点间的实际距离。
应用:这一公式广泛应用于物理学中的一维运动分析、统计学中的数据分布度量、计算机图形学中的点云处理等领域。
公式背后的逻辑与推导
虽然上述公式形式简单,但其背后蕴含了基本的几何与代数原理。在坐标轴上,两点间的距离实际上就是它们坐标之差的绝对值。这一结论可以直接从线段长度的几何定义推导出来。考虑两点A和B在数轴上的位置,A在左,B在右(或反之),那么线段AB的长度就是B的坐标减去A的坐标(或反之,然后取绝对值)。
拓展至二维及三维空间
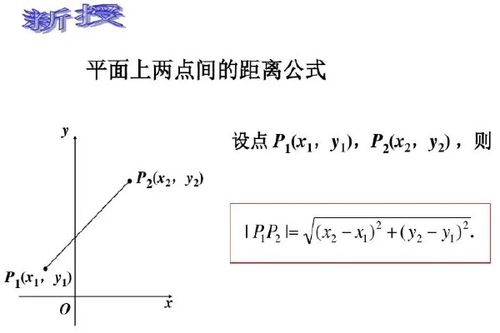
虽然本文聚焦于坐标轴上两点间的距离公式,但了解其在更高维度空间中的推广也颇有意义。在二维空间中(如平面直角坐标系),两点$P_1(x_1, y_1)$和$P_2(x_2, y_2)$之间的距离$d$使用勾股定理计算:
$$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$
而在三维空间中,若两点坐标为$P_1(x_1, y_1, z_1)$和$P_2(x_2, y_2, z_2)$,则距离公式为:
$$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$$
这些公式展示了从简单到复杂,从一维到多维的平滑过渡,体现了数学概念的普遍性和深邃性。
实际应用案例
1. 物理运动分析:在物理学中,当分析物体在一维直线上的运动时,常需计算物体在不同时刻或不同位置之间的距离,坐标轴上两点间距离公式便是基础工具。
2. 图形界面开发:在计算机图形学及用户界面设计中,确定屏幕上元素(如按钮、图标)之间的距离,有助于优化布局,提升用户体验。
3. 数据分析与统计:在统计学中,通过计算数据点之间的“距离”(如曼哈顿距离、欧几里得距离等,虽不完全等同于坐标轴上的距离,但思想相通),可以分析数据间的相似性或差异性。
结语
坐标轴上两点间距离公式,作为连接代数计算与几何直观理解的纽带,其简洁性与实用性在多个领域发挥着不可替代的作用。从基本概念的介绍到实际应用的探讨,我们不难发现,这一简单的公式背后蕴含着丰富的数学原理与广泛的应用前景。随着学习的深入,我们将更加深刻地理解到,数学不仅仅是抽象的符号游戏,更是解决实际问题、探索自然规律的有力武器。
-
 揭秘!两点间距离公式的神奇奥秘,让距离计算变得如此简单新闻资讯10-23
揭秘!两点间距离公式的神奇奥秘,让距离计算变得如此简单新闻资讯10-23 -
 揭秘!直角坐标系中两点距离计算的神秘公式,你知道吗?新闻资讯10-23
揭秘!直角坐标系中两点距离计算的神秘公式,你知道吗?新闻资讯10-23 -
 轻松学会:如何计算斜率新闻资讯10-26
轻松学会:如何计算斜率新闻资讯10-26 -
 探索多种求解斜率k的神奇公式!新闻资讯11-13
探索多种求解斜率k的神奇公式!新闻资讯11-13 -
 95度酒精快速稀释为75度的超简单方法新闻资讯04-02
95度酒精快速稀释为75度的超简单方法新闻资讯04-02 -
 揭秘!长度单位间的神奇进率是多少?新闻资讯10-28
揭秘!长度单位间的神奇进率是多少?新闻资讯10-28












