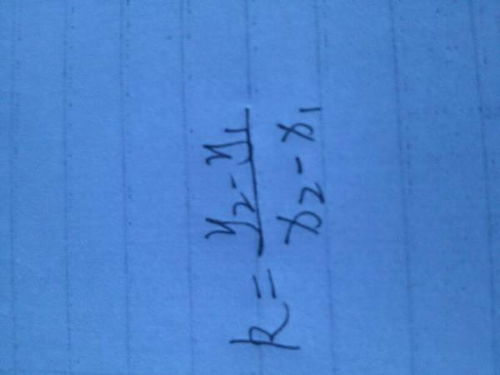轻松学会:如何计算斜率
在探讨“斜率怎么算”这一数学问题时,我们实际上是在深入一个既基础又广泛应用的数学概念。斜率,作为直线在平面直角坐标系中的一个基本属性,不仅在数学学科内部有着举足轻重的地位,而且在物理、工程、经济等多个领域也频繁出现,成为连接理论与实践的重要桥梁。本文将从定义出发,通过几何方法、代数公式、实际应用及图形软件辅助等多个维度,全面解析斜率的计算方法。
一、斜率的定义
斜率是描述一条直线倾斜程度的量度,它表示直线上升或下降的速率。在数学上,斜率定义为直线上任意两点间纵坐标差与横坐标差之商。设直线上有两点A(x₁, y₁)和B(x₂, y₂),且x₁ ≠ x₂,则直线的斜率k可由下式计算得出:

k = (y₂ - y₁) / (x₂ - x₁)
这个公式简洁明了,是求解斜率最直接的方法。需要注意的是,当x₁ = x₂时,两点横坐标相同,意味着这两点位于同一条垂直线上,此时直线斜率不存在(或说斜率为无穷大)。
二、几何方法求解斜率
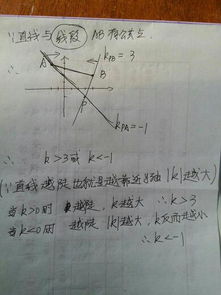
几何方法是一种直观理解斜率的方式,尤其适用于视觉学习者。在平面直角坐标系中,斜率可以被视为直线与x轴正方向的夹角θ的正切值,即tan(θ) = k。通过这一关系,我们可以利用三角函数的性质来求解斜率。
1. 利用正切函数:在已知直线上的一个点和直线与x轴的夹角θ时,斜率k可直接通过tan(θ)求得。这种方法适用于能够直观判断或测量出夹角θ的情况。
2. 通过观察图形:在图形上直接画出直线,然后估算或测量直线与x轴正方向的夹角,再利用三角函数表或计算器求出tan值,即为斜率。这种方法虽然存在误差,但在缺乏精确计算工具时,是一种快速估算斜率的有效手段。
三、代数公式法
代数公式法是求解斜率最常用也是最精确的方法,特别是当直线方程已知时。直线方程有多种形式,每种形式下斜率的求解方式略有不同。
1. 斜截式方程y = mx + b:在这种形式下,斜率k直接等于系数m。斜截式方程直观地表示了直线与y轴的截距b和斜率m的关系,是求解斜率最直接的方式。
2. 两点式方程:如前所述,当知道直线上的两点时,可以直接代入斜率公式k = (y₂ - y₁) / (x₂ - x₁)计算斜率。两点式方程本质上就是斜率公式的应用。
3. 一般式方程Ax + By + C = 0:在一般式方程中,斜率k需要通过变形求解,即k = -A/B。这一转换过程虽然稍显复杂,但一旦掌握,就能灵活应用于各种直线方程。
四、实际应用中的斜率
斜率不仅仅是一个抽象的数学概念,它在现实世界中有着广泛的应用。以下是一些典型例子:
1. 物理学中的斜率:在物理学中,斜率常被用来描述物理量之间的关系。例如,在速度-时间图像中,斜率代表加速度;在位移-时间图像中,斜率代表速度。这些应用使得斜率成为连接物理现象与数学模型的桥梁。
2. 经济学中的斜率:在经济学中,斜率也扮演着重要角色。例如,在需求曲线或供给曲线上,斜率反映了价格变动对需求量或供给量的影响程度。通过对斜率的分析,经济学家可以预测市场行为和政策效果。
3. 工程学中的斜率:在工程设计中,斜率常用于描述结构的倾斜度、地面的坡度等。合理的斜率设计对于保证结构的稳定性和安全性至关重要。
五、图形软件辅助计算斜率
随着科技的发展,图形软件成为求解斜率的新工具。这些软件不仅能够绘制出精确的平面直角坐标系和直线方程,还能自动计算并显示直线的斜率。
1. 数学绘图软件:如GeoGebra、Desmos等,这些软件允许用户输入直线方程,然后自动绘制出直线,并在图形上标注出斜率。用户还可以通过调整方程参数,动态观察斜率的变化。
2. 数据处理软件:在数据分析领域,Excel、SPSS等软件也提供了计算斜率的功能。用户只需输入数据点,软件就能根据线性回归等方法计算出最佳拟合直线的斜率。
3. 专业绘图软件:如AutoCAD、SolidWorks等,这些软件主要用于工程设计领域,能够精确绘制出各种形状和尺寸的图形。通过测量工具,用户可以方便地计算出直线的斜率。
结语
综上所述,斜率的计算方法多种多样,既有基于定义的
- 上一篇: 户口所在地应该如何填写?
- 下一篇: 轻松掌握!微信来电铃声更换与设置指南
-
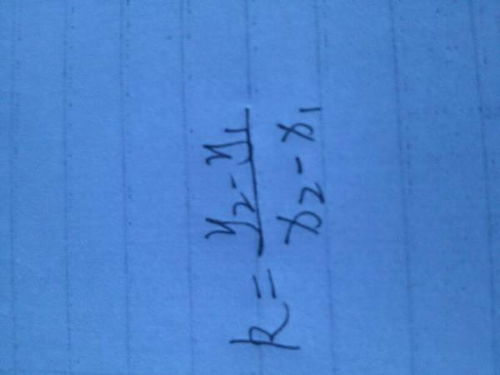 斜率的定义及公式是什么新闻资讯11-13
斜率的定义及公式是什么新闻资讯11-13 -
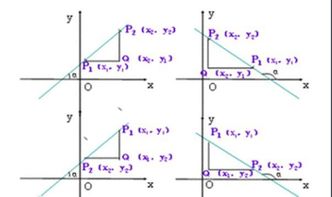 探索多种求解斜率k的神奇公式!新闻资讯11-13
探索多种求解斜率k的神奇公式!新闻资讯11-13 -
 分数求导的奥秘与技巧新闻资讯11-05
分数求导的奥秘与技巧新闻资讯11-05 -
 轻松学会:如何计算扇形的弧长新闻资讯11-05
轻松学会:如何计算扇形的弧长新闻资讯11-05 -
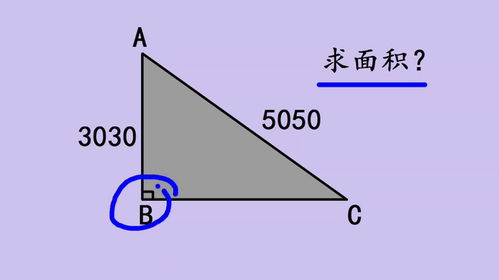 轻松学会!三角形面积的计算方法新闻资讯10-29
轻松学会!三角形面积的计算方法新闻资讯10-29 -
 轻松学会!制作抖音热门年龄计算器视频教程新闻资讯11-19
轻松学会!制作抖音热门年龄计算器视频教程新闻资讯11-19