揭秘!轻松掌握求解最小公倍数的绝招
在学习数学的过程中,掌握求解最小公倍数(Least Common Multiple, LCM)的技巧是一项基础而重要的能力。它不仅能帮助我们解决日常生活中的实际问题,如分配物品、制定时间表等,还是进一步学习分数运算、比例关系以及更高级数学理论的基础。下面,我们将以直接、高效的方式,介绍几种求解最小公倍数的方法,旨在让对此感兴趣的朋友能够快速上手。

一、理解最小公倍数的概念
首先,明确什么是最小公倍数。对于任意两个正整数a和b,存在一个最小的正整数m,它能被a和b同时整除,且这样的m是唯一的,我们称m为a和b的最小公倍数。例如,对于数字4和6,它们的最小公倍数是12,因为12能被4和6同时整除,并且是满足这一条件的最小数。
二、列举法(适用于较小数)
对于较小的两个数,最直接的方法是列举法。即列出两个数的倍数,直到找到第一个共同的倍数,这个倍数就是它们的最小公倍数。以4和6为例:
4的倍数有:4, 8, 12, 16, 20, ...
6的倍数有:6, 12, 18, 24, ...
观察发现,4和6的第一个共同倍数是12,因此,4和6的最小公倍数是12。
三、分解质因数法
对于较大的数,列举法可能效率较低。此时,分解质因数法是一个更有效的方法。首先,将每个数分解为质因数的乘积,然后取各质因数的最高次幂相乘,得到的结果即为这两个数的最小公倍数。
例如,求12和15的最小公倍数:
将12分解质因数:$12 = 2^2 \times 3$
将15分解质因数:$15 = 3 \times 5$
取每个质因数的最高次幂相乘:$LCM(12, 15) = 2^2 \times 3 \times 5 = 60$
四、短除法
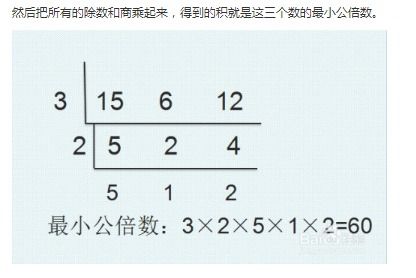
短除法是基于分解质因数法的一种简便形式,特别适合于手动计算。通过短除两个数的公共质因数,直到它们变为互质数(即最大公约数为1的数),然后将所有除数和最后得到的两个互质数相乘,即可得到最小公倍数。
例如,求48和72的最小公倍数:
1. 使用短除法,先找出它们的最大公约数(虽然这里我们直接求LCM,但过程类似,只是最终处理方式不同)。
48和72都可以被2整除,得24和36;
24和36还可以被2整除,得12和18;
12和18都可以被2和3整除,得2和3(此时它们互质)。
2. 将所有除数(包括最后一步的2和3,但通常不包括最后一步的互质数)相乘,并乘以最后的互质数的乘积(在这里是2×3,但因为我们要直接求LCM,所以只需乘除数):
除数有2, 2, 2, 3, 3(注意每个质因数出现的次数)
因此,$LCM(48, 72) = 2^3 \times 3^2 = 8 \times 9 = 72$
五、使用公式(特别情况下)
对于某些特殊情况,我们可以直接利用公式快速求解。比如,当两个数是连续的自然数时,它们的最小公倍数就是这两个数的乘积除以它们的最大公约数(在这种情况下,最大公约数通常为1)。但对于大多数情况,直接应用上述的分解质因数法或短除法更为通用和高效。
六、实际应用
最小公倍数在日常生活和学习中有着广泛的应用。比如:
时间规划:当你需要确定两个不同周期事件的共同发生时间时,可以利用最小公倍数来确定。
资源分配:在分组活动中,如果每组人数不同,需要计算每组至少需要多少物品才能确保每个物品都被均匀分配时,最小公倍数能提供帮助。
分数运算:在分数的加减运算中,为了找到通分母,常常需要求解分母的最小公倍数。
结语
掌握求解最小公倍数的方法,不仅能让我们的数学能力得到提升,还能在实际生活中解决诸多问题。通过上述介绍,无论是通过列举法、分解质因数法、短除法,还是利用特定公式,相信您已经能够灵活应对求解最小公倍数的需求了。希望这篇文章对您有所帮助,激发您对数学的更多兴趣!
- 上一篇: 家中卫生间漏水怎么办?防水补漏实用指南
- 下一篇: 探索'Sea'的英文奥秘:大海的词汇之旅
-
 如何高效求解两个或多个数的最小公倍数?方法总结与技巧分享新闻资讯10-22
如何高效求解两个或多个数的最小公倍数?方法总结与技巧分享新闻资讯10-22 -
 如何快速求解两个数的最小公倍数?详细步骤揭秘!新闻资讯10-23
如何快速求解两个数的最小公倍数?详细步骤揭秘!新闻资讯10-23 -
 如何求解两个数的最小公倍数?新闻资讯10-23
如何求解两个数的最小公倍数?新闻资讯10-23 -
 如何计算两个数的最小公倍数?新闻资讯10-22
如何计算两个数的最小公倍数?新闻资讯10-22 -
 揭秘!轻松掌握求解函数驻点的绝妙方法新闻资讯10-25
揭秘!轻松掌握求解函数驻点的绝妙方法新闻资讯10-25 -
 揭秘!掌握lung单词读音的三大速记绝招,轻松搞定发音难题!新闻资讯10-29
揭秘!掌握lung单词读音的三大速记绝招,轻松搞定发音难题!新闻资讯10-29