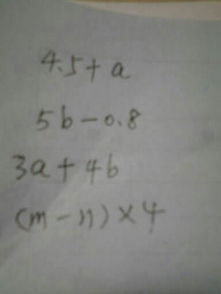如何计算两个数的最小公倍数?
在数学的广阔天地里,最小公倍数(Least Common Multiple, LCM)是一个既基础又实用的概念,它广泛应用于分数运算、日期计算、程序设计等多个领域。理解并掌握求解最小公倍数的方法,对于提升数学素养和解决实际问题具有重要意义。本文将从定义理解、传统算法、公式法、利用最大公约数(Greatest Common Divisor, GCD)的关系以及实际应用等几个维度,深入探讨如何求解最小公倍数。
一、定义理解:何为最小公倍数
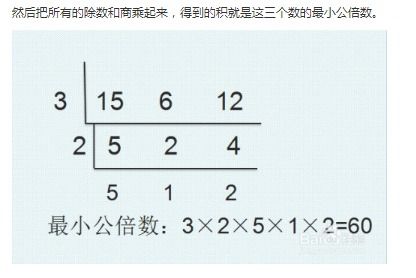
首先,我们需要明确最小公倍数的定义。对于两个或多个整数,如果存在一个最小的正整数,它能够同时被这些整数整除,那么这个数就被称为这些数的最小公倍数。例如,对于数字12和15,它们都可以被60整除,且60是满足这一条件的最小数,因此60是12和15的最小公倍数。

二、传统算法:列举法
对于较小的数,我们可以采用列举法来找出它们的最小公倍数。这种方法虽然直观,但效率较低,特别是当涉及的数字较大时。具体做法是:首先列出两个数的所有倍数,然后从中找出第一个共同的倍数,这个数就是它们的最小公倍数。例如,求12和15的最小公倍数,可以列出12的倍数:12, 24, 36, 48, 60...;再列出15的倍数:15, 30, 45, 60...;发现60是第一个共同的倍数,因此LCM(12, 15) = 60。
三、公式法:直接计算
虽然列举法直观易懂,但对于较大的数或需要快速计算时,就显得力不从心了。此时,我们可以利用一些数学公式来直接计算最小公倍数。不过,值得注意的是,直接用于计算最小公倍数的简单公式并不常见,但我们可以利用最大公约数(GCD)与最小公倍数之间的关系来间接求解。这一关系基于一个重要的数学定理:两数的乘积等于它们的最大公约数与最小公倍数的乘积。即:
\[ a \times b = \text{GCD}(a, b) \times \text{LCM}(a, b) \]
由此,我们可以推导出求最小公倍数的公式:
\[ \text{LCM}(a, b) = \frac{a \times b}{\text{GCD}(a, b)} \]
四、利用最大公约数的关系
既然提到了最大公约数与最小公倍数的关系,那么我们就不得不深入探讨一下如何利用最大公约数来求解最小公倍数。这通常涉及到一个高效的算法——欧几里得算法(Euclidean Algorithm),该算法主要用于计算两个整数的最大公约数。一旦我们得到了最大公约数,就可以轻松地利用上述公式计算出最小公倍数。
欧几里得算法的基本思想是:对于两个正整数a和b(假设a>b),它们的最大公约数等于b和a除以b的余数(记作c)的最大公约数。即gcd(a, b) = gcd(b, a mod b),不断重复这一过程,直到余数为0,此时的非零除数即为所求的最大公约数。
五、实际应用:场景举例
1. 分数加减
在分数的加减运算中,通常需要找到两个分数的最小公倍数作为通分的分母,以确保运算的正确性。例如,计算1/2 + 1/3,首先找到2和3的最小公倍数6,然后将两个分数转换为以6为分母的形式,即3/6 + 2/6 = 5/6。
2. 日期计算
在日常生活中,我们可能会遇到需要计算两个日期之间的天数,特别是当这两个日期分别落在不同的月份或年份时,最小公倍数的概念就显得尤为重要。虽然直接计算日期差通常不直接用到LCM,但在处理周期性事件(如某活动每N年举行一次,另一活动每M年举行一次,求两者同时举行的最小间隔年数)时,LCM的概念就派上了用场。
3. 程序设计
在程序设计中,尤其是在处理数组、循环等结构时,了解最小公倍数可以帮助我们优化算法,减少不必要的迭代或内存占用。例如,在生成特定频率的波形时,可能需要确保采样率能够同时满足多个信号源的需求,此时就需要计算这些信号源频率的最小公倍数作为采样率。
结语
综上所述,最小公倍数是数学中一个非常重要的概念,它不仅在理论学习中占据一席之地,更在实际应用中发挥着不可替代的作用。通过理解其定义、掌握求解方法(包括传统算法、公式法以及利用最大公约数的关系),我们可以更加灵活地运用这一工具解决各种问题。同时,将理论知识与实际应用相结合,也是提升数学素养和解决问题能力的重要途径。
- 上一篇: 全面的百家姓列表概览
- 下一篇: 一键开启微信运动,轻松记录每日步数
-
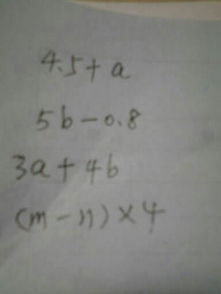 如何求解两个数的最小公倍数?新闻资讯10-23
如何求解两个数的最小公倍数?新闻资讯10-23 -
 如何快速求解两个数的最小公倍数?详细步骤揭秘!新闻资讯10-23
如何快速求解两个数的最小公倍数?详细步骤揭秘!新闻资讯10-23 -
 如何高效求解两个或多个数的最小公倍数?方法总结与技巧分享新闻资讯10-22
如何高效求解两个或多个数的最小公倍数?方法总结与技巧分享新闻资讯10-22 -
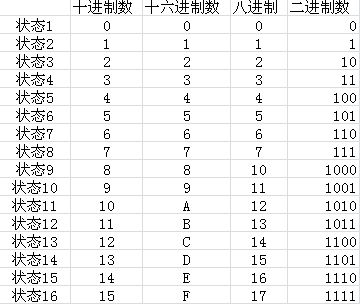 轻松掌握:二进制与十六进制数的相互转换方法新闻资讯11-07
轻松掌握:二进制与十六进制数的相互转换方法新闻资讯11-07 -
 揭秘中位数计算奥秘:从乱序到有序,一步步找到数据的平衡点新闻资讯10-27
揭秘中位数计算奥秘:从乱序到有序,一步步找到数据的平衡点新闻资讯10-27 -
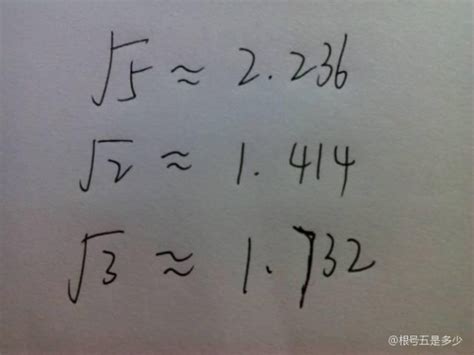 根号5的精确值及计算方法新闻资讯10-28
根号5的精确值及计算方法新闻资讯10-28