揭秘!轻松掌握求解函数驻点的绝妙方法
函数的驻点怎么求
在数学领域,尤其是微积分学中,驻点(又称平稳点、稳定点或临界点)是一个极其重要的概念。简而言之,驻点就是函数一阶导数为零的点,即在这一点上,函数的输出值停止增加或减少。对于初学者或是对此感兴趣的朋友来说,了解如何求解函数的驻点,不仅能帮助深入理解函数性质,还能为后续的极值分析、优化问题求解等打下坚实的基础。
一、驻点的定义与性质
首先,我们明确驻点的定义:在数学上,驻点是指函数一阶导数为零的点。这意味着在这一点,函数图像不再上升或下降,而是保持水平或转向新的增减趋势。对于一维函数,驻点处的切线平行于x轴;对于二维函数,驻点处的切平面则平行于xy平面。

值得注意的是,驻点并不一定就是函数的极值点。在某些情况下,即使函数的一阶导数为零,但如果在这一点左右两侧一阶导数的符号没有改变,那么该点就不是极值点。同样,在特定区域内,一个函数的极值点也不一定就是驻点,这取决于边界条件等额外因素。

二、求解驻点的步骤
求解函数的驻点,本质上就是寻找使得函数一阶导数等于零的x值。以下是具体的求解步骤:
1. 求函数的一阶导数:
首先,我们需要对给定的函数进行求导,得到其一阶导数表达式。这一步是基础且必要的,因为驻点正是由一阶导数等于零的条件定义的。
2. 令一阶导数等于零:
将一阶导数表达式设为等于零,得到一个关于x的方程。这个方程将帮助我们找到可能的驻点。
3. 解方程求解x值:
解这个一阶导数等于零的方程,得到x的解。这些解就是函数可能的驻点。
4. 验证解的有效性:
有时候,解出的x值可能不在函数的定义域内,或者在该点处函数不可导(如存在尖点、断点等)。因此,我们需要验证解出的x值是否确实对应有效的驻点。
三、示例解析
为了更好地理解驻点的求解过程,我们通过几个具体的例子来进行说明。
例1:
给定函数 $f(x) = x^2 - 4x + 3$,求其驻点。
求解过程:
1. 求一阶导数:
$f'(x) = 2x - 4$
2. 令一阶导数等于零:
$2x - 4 = 0$
3. 解方程求解x值:
$x = 2$
因此,$x = 2$ 是函数 $f(x) = x^2 - 4x + 3$ 的驻点。
例2:
考虑函数 $g(x) = \cos x + \frac{x}{2}$,求其驻点。
求解过程:
1. 求一阶导数:
利用三角函数的导数公式和线性函数的导数规则,得到
$g'(x) = -\sin x + \frac{1}{2}$
2. 令一阶导数等于零:
$-\sin x + \frac{1}{2} = 0$
3. 解方程求解x值:
由于这是一个超越方程,无法直接求解出x的解析表达式。但我们可以利用三角函数的性质,得到x的近似解或一般解形式。具体来说,该方程的解为
$x = 2k\pi + \frac{\pi}{6}$ 和 $x = 2k\pi + \frac{5\pi}{6}$,其中 $k \in \mathbb{Z}$。
因此,这些x值就是函数 $g(x) = \cos x + \frac{x}{2}$ 的驻点。
四、结语
通过上述介绍和示例解析,我们可以看到求解函数的驻点并不复杂,关键在于理解驻点的定义和性质,并熟练掌握函数求导的方法。一旦掌握了这些基本技能和知识,我们就可以轻松地找到函数的驻点,并进一步分析函数的极值、单调性等重要性质。希望本文能够激发你对函数驻点求解的兴趣,并为你后续的学习和研究提供帮助。
-
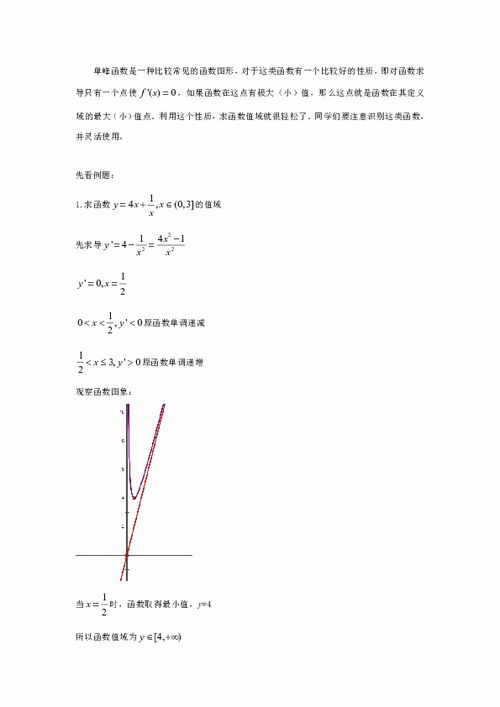 掌握函数值域的多种高效求解技巧新闻资讯05-26
掌握函数值域的多种高效求解技巧新闻资讯05-26 -
 揭秘!什么是驻点?一文带你深入了解这一重要概念新闻资讯10-25
揭秘!什么是驻点?一文带你深入了解这一重要概念新闻资讯10-25 -
 如何求解偏导数?新闻资讯11-23
如何求解偏导数?新闻资讯11-23 -
 分数的导数求解方法新闻资讯11-05
分数的导数求解方法新闻资讯11-05 -
 掌握IF函数的绝妙用法,轻松实现数据条件判断新闻资讯10-22
掌握IF函数的绝妙用法,轻松实现数据条件判断新闻资讯10-22 -
 揭秘:如何在计算器上轻松操作arctan函数新闻资讯11-02
揭秘:如何在计算器上轻松操作arctan函数新闻资讯11-02