揭秘有理数的神秘面纱
在我们日常生活中,数学无处不在,它帮助我们理解世界,解决问题。今天,我们要聊的是一个既熟悉又可能略带神秘感的数学概念——有理数。别担心,即使你对数学不是特别感冒,读完这篇文章后,你也会对有理数有一个清晰而深刻的认识。

首先,让我们从“有理数”这个名字开始。听到“有理”,你可能会想到合理、有道理的意思,但在数学里,它其实是指可以表示为两个整数之比的数。换句话说,如果一个数可以写成a/b(a和b都是整数,且b不为0)的形式,那么这个数就是有理数。
有理数的由来
有理数这个名字来源于古希腊数学家毕达哥拉斯学派的一个故事。毕达哥拉斯学派非常注重数与形的关系,他们认为万物皆数。然而,当他们试图用整数或整数之比来解释正方形的对角线长度时,遇到了难题。他们发现,对角线的长度无法表示为两个整数的比,这违背了他们的信念,因此他们称这样的数为“无理数”,而与之相对的,那些可以表示为整数之比的数,就被称为“有理数”。
有理数的分类
有理数其实是一个大家庭,里面包括了正有理数、负有理数和0。
正有理数:就是大于0的有理数,比如1/2、3/4、7/8等。它们都可以表示为两个正整数的比,或者一个正整数和一个负整数的比(但结果为正),只要分母不为0。
负有理数:小于0的有理数,比如-1/2、-3/4、-7/8等。它们可以看作是正有理数的相反数。
0:虽然0看起来很简单,但它也是有理数的一员。因为0可以看作是任何非零整数与0的比(虽然这种表示方式在数学上并不严谨,但可以帮助我们理解0属于有理数的范畴)。更正式地说,0可以表示为0/b(b≠0)的形式,满足有理数的定义。
有理数的性质
有理数具有一些有趣的性质,这些性质让我们能够更好地理解和运用它们。
封闭性:有理数与有理数进行加、减、乘、除(除数不为0)运算后,结果仍然是有理数。这意味着有理数集在四则运算下是封闭的。
稠密性:在任意两个有理数之间,总可以找到一个新的有理数。比如,在1/2和1之间,我们可以找到3/4、5/8等无数个有理数。这种性质使得有理数在数轴上分布得非常密集。
可表示性:正如我们之前提到的,有理数都可以表示为两个整数的比。这种表示方式让我们能够直观地看到有理数与整数之间的关系。
有理数与无理数的区别
既然我们已经了解了有理数,那么与之相对的无理数又是什么呢?简单来说,无理数就是不能表示为两个整数之比的数。无理数在数轴上也是无限不循环的小数,比如π(圆周率)、e(自然对数的底数)和√2(2的平方根)等。
有理数与无理数的最大区别在于它们的十进制表示。有理数的十进制表示要么是有限小数,要么是无限循环小数;而无理数的十进制表示则是无限不循环小数。这个区别让我们能够轻松地区分一个数是有理数还是无理数。
有理数的实际应用
有理数在我们的日常生活中有着广泛的应用。无论是购物时的价格计算,还是烹饪时的配料比例,甚至是科学研究中的数据分析,都离不开有理数的身影。
金融领域:在股票交易、利率计算等方面,有理数帮助我们精确计算成本和收益。
工程领域:在设计建筑、桥梁等结构时,工程师需要使用有理数来计算尺寸、重量和强度等参数。
物理学:在物理学中,有理数用于描述物体的运动状态、能量转换等物理现象。
日常生活:比如我们常说的“一半”(1/2)、“三分之一”(1/3)等,都是有理数的实际应用。
如何判断一个数是有理数
判断一个数是否有理数,通常有两种方法:
1. 直接判断法:观察这个数的十进制表示。如果它是有限小数或无限循环小数,那么它就是有理数;如果它是无限不循环小数,那么它就是无理数。
2. 代数法:尝试将这个数表示为两个整数的比。如果能够成功表示,并且分母不为0,那么这个数就是有理数;如果无法表示或表示后分母为0(在数学上,0不能作为除数),那么这个数就可能是无理数(当然,有些数可能需要通过更复杂的代数方法或数学证明才能确定其是否为有理数)。
结语
通过上面的介绍,相信你已经对有理数有了比较全面的了解。有理数
- 上一篇: 蓝牙耳机使用教程详解
- 下一篇: Word中轻松打出小于号的方法
-
 实数定义揭秘:究竟何为实数?0是否包含在内?新闻资讯11-06
实数定义揭秘:究竟何为实数?0是否包含在内?新闻资讯11-06 -
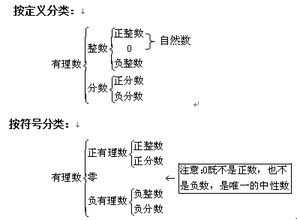 什么是有理数?请举例说明。新闻资讯11-12
什么是有理数?请举例说明。新闻资讯11-12 -
 分式的定义及详细解释新闻资讯11-23
分式的定义及详细解释新闻资讯11-23 -
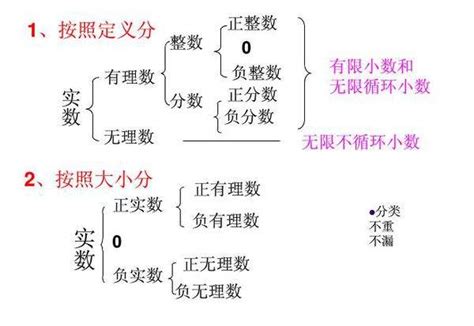
 全面解析:什么是实数?请举例说明新闻资讯11-06
全面解析:什么是实数?请举例说明新闻资讯11-06 -
 揭秘!'OCT'究竟代表了哪个月份的神秘面纱新闻资讯10-24
揭秘!'OCT'究竟代表了哪个月份的神秘面纱新闻资讯10-24 -
 《天涯明月刀》揭秘:公子羽神秘面纱下的真实身份究竟是谁?新闻资讯02-20
《天涯明月刀》揭秘:公子羽神秘面纱下的真实身份究竟是谁?新闻资讯02-20