什么是有理数？请举例说明。

在我们日常的数学学习和生活中，经常会听到“有理数”这个词。那么，有理数到底是什么意思呢？它涵盖了哪些具体的数字呢？今天，我们就来一起揭开有理数的神秘面纱，让它变得通俗易懂。

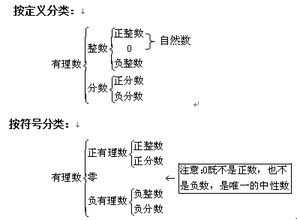
首先，我们来明确一下有理数的定义。有理数，顾名思义，就是“有道理”的数。这里的“道理”其实是指这些数都可以表示成两个整数的比（分数）形式。换句话说，有理数是可以被精确表示的，不会有无穷无尽的小数位。具体来说，如果两个整数a和b（b不等于0）相除，得到的商就是有理数，记作a/b。

了解了定义之后，我们来看看哪些常见的数属于有理数。

整数

首先，最简单也最直接的一类有理数就是整数。整数包括正整数（如1, 2, 3,...）、零和负整数（如-1, -2, -3,...）。这些整数都可以看作是分母为1的分数，例如整数3可以写成3/1，因此整数是有理数的一个子集。

正有理数和负有理数

除了整数之外，有理数还包括分数。分数可以是正的，也可以是负的。例如，1/2和-3/4都是有理数。这里需要注意的是，即使分数的分子和分母都是负数，最终得到的结果仍然是有理数，只不过正负号会根据分子和分母的符号来确定。例如，-1/-2等于1/2，结果为正有理数。

有限小数和无限循环小数

另一个帮助我们理解有理数的重要特征是，有理数都可以表示为有限小数或无限循环小数。有限小数是指小数点后只有有限位数字的数，比如0.5、1.25和7.333。无限循环小数是指小数点后某一段数字无限重复的数，比如1/3等于0.333...，其中3无限循环。

例子解析

为了更好地理解有理数，让我们通过一些具体的例子来加以说明。

0.75：这是一个有限小数，可以表示为3/4，因此是有理数。

1.666...（6无限循环）：这是一个无限循环小数，可以表示为5/3，因此也是有理数。

2/3：这是一个负分数，可以转换为小数形式-0.666...，其中6无限循环，因此也是有理数。

0：这是整数，可以看作是0/1或任何形式a/a（a不等于0），因此也是有理数。

有理数的运算

有理数的另一个特点是，它们支持基本的算术运算，包括加法、减法、乘法和除法（除数不为零）。这些运算的结果仍然是有理数。例如：

加法：1/2 + 1/4 = 2/4 + 1/4 = 3/4

减法：3/4 - 1/2 = 3/4 - 2/4 = 1/4

乘法：1/3 * 2/5 = 2/15

除法：2/3 ÷ 1/4 = 2/3 * 4/1 = 8/3

有理数与无理数的区别

为了更全面地理解有理数，我们还需要知道它与无理数的区别。无理数是指那些无法表示为两个整数之比的数，即无法写成分数形式的数。无理数的小数部分是无限不循环的。最常见的无理数包括圆周率π（约等于3.14159...）和自然对数的底数e（约等于2.71828...）。此外，像根号2、根号3等无法开方得到整数的平方根也是无理数。

有理数在日常生活中的应用

有理数不仅在数学学科中占据重要地位，而且在我们的日常生活中也有着广泛的应用。例如，我们在购物时计算折扣、分配食物时的比例、设置闹钟的时间以及量度物体的尺寸时，都会用到有理数。

购物：假设一件原价100元的商品打七折，那么折扣后的价格就是70元。这里的七折可以用有理数0.7来表示。

烹饪：当你需要按照食谱将食材分成三份时，每一份的比例就是1/3，这也是有理数。

时间：当我们设定闹钟为6点30分时，这个时间点可以用有理数6.5小时（将分钟转换为小时的小数形式）来表示。

测量：当我们用尺子测量一个物体的长度为1.5厘米时，这也是有理数。

有理数的扩展——十进制有理数与有理数的表示

在数学中，有理数不仅限于十进制形式，它们还可以在二进制、八进制和十六进制等不同的数制中表示。虽然