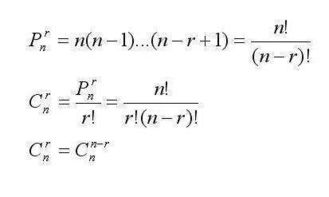揭秘组合数学的核心公式
在数学领域中,组合是一个核心概念,它涉及到从一组元素中选取部分元素而不考虑顺序的问题。组合的公式是什么,这一问题是初学者常常提出的疑问。为了深入理解这一概念,我们需要从基础开始,逐步探讨组合的定义、性质以及公式的推导过程。

首先,我们需要明确组合的基本概念。组合是从n个不同元素中取出m(m≤n)个元素的所有取法。与排列不同,组合不考虑取出的元素的顺序。例如,从集合{1,2,3}中取出两个元素的组合有{1,2},{1,3},{2,3},而{1,2}和{2,1}在组合中被视为同一种情况。

组合的公式表示为C(n,m),读作“n选m”,其计算公式为C(n,m)=n!/[m!(n-m)!]。这里,n!表示n的阶乘,即n×(n-1)×...×2×1。公式的含义是从n个元素中选出m个元素的组合数,等于n的阶乘除以m的阶乘与(n-m)的阶乘的乘积。这个公式是组合数学中的基础,它为我们提供了一种计算组合数的方法。

为了更直观地理解这个公式,我们可以考虑一个具体的例子。假设我们有一个包含5个元素的集合,我们想要从中选出3个元素。根据组合的公式,我们可以计算出C(5,3)=5!/[3!(5-3)!]=5×4×3×2×1/(3×2×1×2×1)=10。这意味着从5个元素中选出3个元素的组合有10种可能。

接下来,我们探讨组合的一些基本性质。首先,组合数具有对称性,即C(n,m)=C(n,n-m)。这是因为从n个元素中选出m个元素的组合数,与从n个元素中选出(n-m)个元素的组合数是相同的。例如,C(5,3)=C(5,2)=10,因为从5个元素中选出3个元素的组合数与从5个元素中选出2个元素的组合数相同。
其次,组合数具有单调性,即当n固定时,C(n,m)随着m的增大而增大,直到m=n/2(当n为偶数时)或m=(n-1)/2(当n为奇数时)达到最大值,然后随着m的继续增大而减小。这是因为当m较小时,可选的元素较多,因此组合数较大;而当m较大时,剩余的元素较少,因此组合数也较小。
此外,组合数还具有可加性,即C(n,m)=C(n-1,m-1)+C(n-1,m)。这个性质表明,从n个元素中选出m个元素的组合数,等于从(n-1)个元素中选出(m-1)个元素的组合数与从(n-1)个元素中选出m个元素的组合数之和。这个性质在组合数学中有着广泛的应用,它为我们提供了一种计算组合数的新方法。
现在,我们来探讨一下组合公式的推导过程。组合的公式C(n,m)=n!/[m!(n-m)!]是如何得出的呢?我们可以通过以下步骤进行推导:
第一步,考虑从n个元素中选出m个元素的所有可能情况。每个元素都有被选中或不被选中的可能,因此总共有2^n种可能的情况。但是,这包括了所有可能的排列和组合,而我们只需要组合数。
第二步,为了得到组合数,我们需要排除所有可能的排列。对于选出的m个元素,它们有m!种不同的排列方式。因此,我们需要将2^n除以m!来排除这些排列。
第三步,我们还需要考虑剩下的(n-m)个元素。这些元素虽然没有被选中,但它们也有(n-m)!种不同的排列方式。因此,我们还需要将上一步的结果除以(n-m)!来排除这些排列。
经过以上三步推导,我们得到了组合的公式C(n,m)=n!/[m!(n-m)!]。这个公式为我们提供了一种计算组合数的方法,它考虑了所有可能的排列和组合,并排除了所有不需要的排列。
组合公式在数学、计算机科学、统计学等领域都有着广泛的应用。例如,在概率论中,组合公式用于计算事件发生的概率;在计算机科学中,组合公式用于算法设计和优化;在统计学中,组合公式用于数据分析和预测。
此外,组合公式还与一些其他数学概念密切相关。例如,组合数与二项式定理有着紧密的联系。二项式定理告诉我们,(a+b)^n的展开式中的每一项的系数都等于C(n,k),其中k是从0到n的整数。这为我们提供了一种计算二项式展开式系数的方法。
- 上一篇: 六国覆灭次序巧记顺口溜揭秘
- 下一篇: 《忍者佐良娜崛起1.13》:全面攻略,解锁强者之路
-
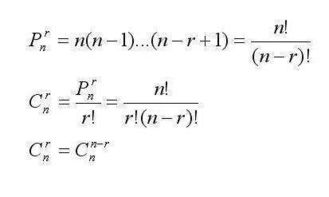 揭秘:概率运算不可或缺的五大核心公式!新闻资讯11-03
揭秘:概率运算不可或缺的五大核心公式!新闻资讯11-03 -
 揭秘:掌握数学精髓,三个不可或缺的中值定理公式详解新闻资讯11-08
揭秘:掌握数学精髓,三个不可或缺的中值定理公式详解新闻资讯11-08 -
 揭秘:概率计算公式的奥秘与应用新闻资讯10-30
揭秘:概率计算公式的奥秘与应用新闻资讯10-30 -
 揭秘:积分中值定理的核心公式大公开!新闻资讯10-25
揭秘:积分中值定理的核心公式大公开!新闻资讯10-25 -
 揭秘!圆形面积的神奇计算公式,一学就会的几何奥秘新闻资讯10-23
揭秘!圆形面积的神奇计算公式,一学就会的几何奥秘新闻资讯10-23 -
 曲率公式的定义是什么新闻资讯10-31
曲率公式的定义是什么新闻资讯10-31