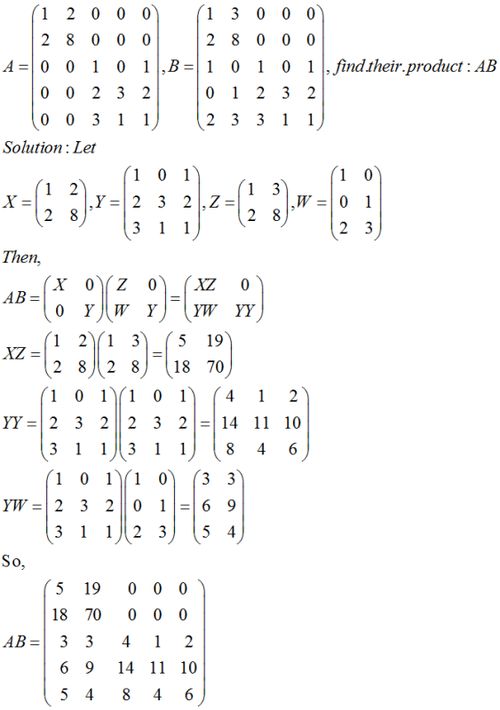揭秘:概率运算不可或缺的五大核心公式!
在概率论这一数学分支中,概率运算占据着核心地位。概率运算不仅帮助我们理解随机事件发生的可能性,还是许多统计分析和决策制定的基础。为了系统地掌握概率运算,五个基本公式显得尤为重要。这些公式包括加法公式、减法公式、乘法公式、条件概率公式和全概率公式。它们各自在不同的情境下发挥着关键作用,构成了概率运算的基石。
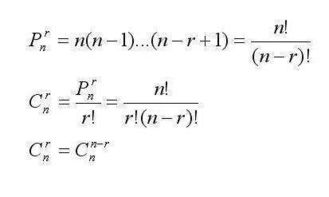
加法公式:概率的合并
加法公式,也称为概率的加法原理或并集公式,用于计算两个或多个事件至少有一个发生的概率。假设有两个事件A和B,事件A发生的概率为P(A),事件B发生的概率为P(B),而事件A和B同时发生的概率为P(A∩B)。根据加法公式,事件A或B(或两者都)发生的概率为:
P(A∪B) = P(A) + P(B) - P(A∩B)
这个公式体现了概率的合并原则,即当两个事件不是互斥(即可以同时发生)时,它们或的关系的概率需要将各自的概率相加,并减去它们同时发生的概率以避免重复计算。如果事件A和B是互斥的,即P(A∩B) = 0,则加法公式简化为P(A∪B) = P(A) + P(B)。
加法公式在解决复杂事件的概率问题时非常有用,特别是当事件之间存在某种重叠时。例如,在医学研究中,我们可能需要计算一个人患有某种疾病或另一种疾病的概率,这时就需要用到加法公式来合并这两种疾病的概率。
减法公式:概率的排除
与加法公式相对应的是减法公式,它用于计算一个事件在另一个事件不发生的条件下的概率。假设我们有两个事件A和B,事件A发生的概率为P(A),事件B发生的概率为P(B),而事件A在事件B不发生的条件下发生的概率为P(A|¬B)(其中¬B表示B不发生)。根据减法公式,我们有:
P(A - B) = P(A) - P(A∩B)
这个公式实际上是从加法公式中推导出来的,当考虑事件A发生而事件B不发生的情况时,相当于计算A发生而B不发生的概率,即P(A)减去A和B同时发生的概率P(A∩B)。
减法公式在解决需要排除某些条件的问题时非常有用。例如,在市场调研中,我们可能需要计算某个产品在不考虑某个特定竞争对手影响下的市场份额,这时就可以使用减法公式来排除该竞争对手的影响。
乘法公式:概率的联合
乘法公式,也称为概率的乘法原理或交集公式,用于计算两个或多个事件同时发生的概率。假设有两个事件A和B,事件A发生的概率为P(A),在事件A发生的条件下事件B发生的概率为P(B|A)。根据乘法公式,事件A和B同时发生的概率为:
P(A∩B) = P(A) × P(B|A)
这个公式体现了概率的联合原则,即一个事件在另一个事件发生的条件下的概率等于这两个事件各自概率的乘积。乘法公式在概率论中非常重要,因为它连接了条件概率和联合概率,使得我们可以在已知某些条件的情况下计算复杂事件的概率。
乘法公式在多个领域都有广泛应用。例如,在通信工程中,我们需要计算信号在传输过程中被正确接收的概率,这时就需要用到乘法公式来联合考虑信号的发送概率和接收概率。
条件概率公式:概率的修正
条件概率公式用于计算在已知某个事件发生的条件下,另一个事件发生的概率。假设有两个事件A和B,事件B发生的概率为P(B),在事件B发生的条件下事件A发生的概率为P(A|B)。根据条件概率公式,我们有:
P(A|B) = P(A∩B) / P(B)
这个公式实际上是对概率的一种修正,它告诉我们当已知某个事件发生时,另一个事件发生的概率应该如何调整。条件概率公式在概率论和统计学中非常重要,因为它允许我们在已知某些信息的情况下更新我们对事件发生的信念。
条件概率公式在决策制定中起着关键作用。例如,在医学诊断中,医生需要根据患者的症状和病史来判断患者患有某种疾病的概率,这时就需要用到条件概率公式来修正疾病的概率。
全概率公式:概率的分解
全概率公式用于计算一个事件在多个互斥且完备的条件下的概率。假设有一个事件A,以及一系列互斥且完备的事件B1, B2, ..., Bn(即这些事件两两不相交且它们的并集是全集),每个事件Bi发生的概率为P(Bi),在事件Bi发生的条件下事件A发生的概率为P(A|Bi)。根据全概率公式
- 上一篇: 如何查询往届高考成绩及查询入口
- 下一篇: 掌握顿号精髓:正确使用与不可忽视的注意事项
-
 揭秘:概率计算公式的奥秘与应用新闻资讯10-30
揭秘:概率计算公式的奥秘与应用新闻资讯10-30 -
 揭秘:概率计算公式全解析新闻资讯10-25
揭秘:概率计算公式全解析新闻资讯10-25 -
 对数运算的公式详解新闻资讯11-23
对数运算的公式详解新闻资讯11-23 -
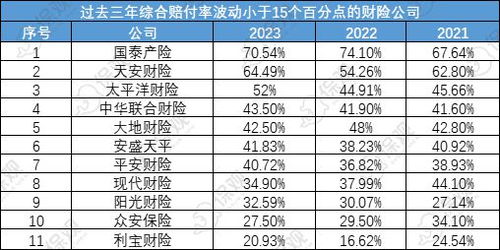 如何计算平赔率与赔付率的具体公式是什么?新闻资讯11-09
如何计算平赔率与赔付率的具体公式是什么?新闻资讯11-09 -
 揭秘:置信区间计算公式的奥秘与实用方法新闻资讯11-12
揭秘:置信区间计算公式的奥秘与实用方法新闻资讯11-12 -
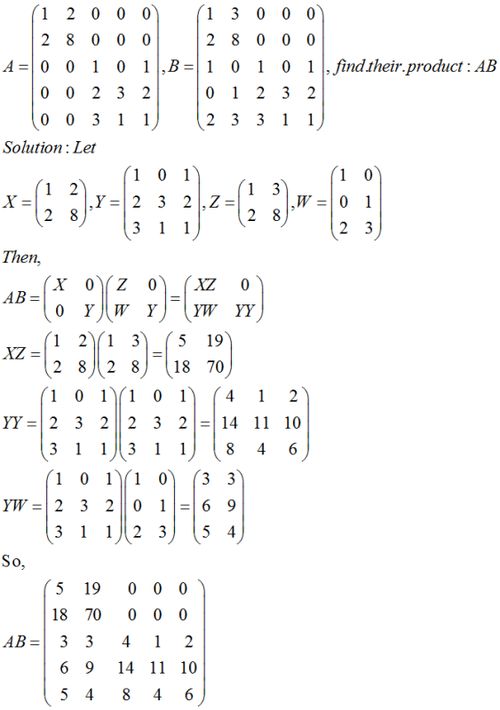 揭秘:矩阵乘法运算的详细步骤新闻资讯12-13
揭秘:矩阵乘法运算的详细步骤新闻资讯12-13