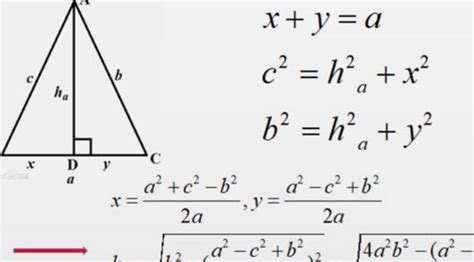三角函数公式有哪些?
在数学的浩瀚宇宙中,三角函数如同一颗璀璨的星辰,不仅照亮了几何与代数的交汇之路,还为物理学、工程学乃至天文学等领域提供了强有力的数学工具。今天,我们就来一场轻松愉快的探索之旅,揭开三角函数公式的神秘面纱,看看它们是如何在直角三角形中翩翩起舞,又在坐标系里编织出绚丽的图案的。

一、初识三角函数:直角三角形的秘密
想象一下,你手中拿着一个标准的直角三角形,它有一个90度的直角,两边分别是邻边(与直角相邻的边)、对边(与直角相对的边),还有一条斜边(最长的那条边)。三角函数,简单来说,就是通过这个三角形的边长关系,来描述角度与边长之间的奇妙联系。

1. 正弦(sine,简称sin)
正弦函数是这样定义的:对于任意角θ(以弧度或度为单位),其对边长度与斜边长度的比值就是sinθ。用公式表示就是:
sinθ = 对边 / 斜边
想象一下,当你慢慢转动这个角,对边的长度会变化,但斜边始终是固定的,所以sinθ的值也会随之改变,反映出了角度和边长之间的动态关系。
2. 余弦(cosine,简称cos)
余弦函数则是邻边长度与斜边长度的比值。公式为:
cosθ = 邻边 / 斜边
与正弦相反,当你改变角度θ时,邻边的长度在变化,而cosθ的值则告诉你这种变化与斜边相比是怎样的。
3. 正切(tangent,简称tan)
正切函数则稍显特别,它是对边长度与邻边长度的比值。公式为:
tanθ = 对边 / 邻边
注意,这里不需要斜边参与计算,但正因为如此,正切函数在θ接近90度(或π/2弧度)时会趋于无穷大,因为此时对边会变得非常长,而邻边则趋于零。
二、从直角到任意角:三角函数的扩展
刚才我们讨论的都是基于直角三角形的三角函数,但实际上,三角函数可以应用于任何角度,包括大于90度的钝角、小于0度的负角,甚至是围绕原点旋转多圈的角。这得益于单位圆的概念。
想象一个半径为1的圆,圆心位于坐标原点(0,0)。在这个圆上,任何一点P(x,y)都可以与某个角度θ对应起来,其中θ是从正x轴逆时针旋转到点P所在射线的角度。此时,点P的x坐标就是cosθ,y坐标就是sinθ。这种定义方式让三角函数超越了直角三角形的限制,成为了一种更加通用和强大的工具。
三、三角函数的周期性与对称性
三角函数不仅是数学美的体现,它们还拥有着迷人的周期性和对称性。
1. 周期性
正弦和余弦函数都是周期函数,周期为2π(360度)。这意味着,如果你在一个完整的周期后再加上或减去2π的任意整数倍,函数值将重复。例如,sin(θ+2π) = sinθ,cos(θ+2π) = cosθ。这种周期性在信号处理、波动分析等领域有着广泛的应用。
正切函数虽然也有周期性,但其周期为π(180度),因为tan(θ+π) = tanθ。
2. 对称性
正弦和余弦函数还具有奇偶性。正弦函数是奇函数,即sin(-θ) = -sinθ,图像关于原点对称;而余弦函数是偶函数,cos(-θ) = cosθ,图像关于y轴对称。正切函数则既没有奇性也没有偶性,但它具有周期性内的对称性,如tan(π/2 - θ) = 1/tanθ。
四、三角函数公式的应用实例
三角函数公式不仅仅是数学书上的抽象概念,它们在实际生活中有着广泛的应用。
1. 物理学中的波动与振动
在物理学中,简谐振动和波动现象可以用正弦或余弦函数来描述。比如,弹簧振子的位移随时间的变化,或者声波在空气中的传播,都可以用三角函数来建模。
2. 工程学中的信号处理
在电子工程中,三角函数被用来分析交流电的信号,如电压和电流的变化。傅里叶变换等工具更是将复杂的信号分解为一系列不同频率的正弦和余弦波,便于分析和处理。
3. 天文学中的运动计算
天文学中,行星、卫星等的运动轨迹和速度变化也常用三角函数来表示。比如,开普勒定律就涉及到椭圆轨道上的角度和距离的关系,这些关系可以用三角函数来精确计算。
五、三角函数的记忆技巧
面对这么多公式和性质,初学者可能会感到有些头疼。不过,别担心,有几个小技巧可以帮助你更好地记忆
- 上一篇: 情感中的难以逾越之鸿沟
- 下一篇: 康熙帝享年多少岁
-
 掌握Excel必备!九大高效函数公式技巧大揭秘新闻资讯10-29
掌握Excel必备!九大高效函数公式技巧大揭秘新闻资讯10-29 -
 三角形面积计算公式详解新闻资讯11-25
三角形面积计算公式详解新闻资讯11-25 -
 无穷小量等价代换的常用公式是什么?新闻资讯12-22
无穷小量等价代换的常用公式是什么?新闻资讯12-22 -
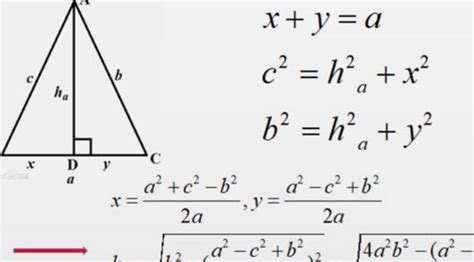 小学五年级学生如何计算三角形面积?请告知公式新闻资讯10-29
小学五年级学生如何计算三角形面积?请告知公式新闻资讯10-29 -
 揭秘对数函数Log的基石:掌握这些基本公式,解锁数学新视界!新闻资讯10-25
揭秘对数函数Log的基石:掌握这些基本公式,解锁数学新视界!新闻资讯10-25 -
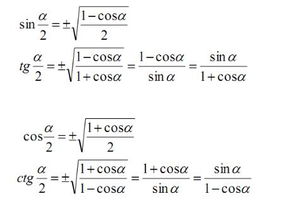 详解半角公式与二倍角公式的定义与应用新闻资讯10-18
详解半角公式与二倍角公式的定义与应用新闻资讯10-18