不规则四边形面积的通用计算公式是什么
在众多几何形状中,不规则四边形因其多变的形态和广泛的应用场景而备受瞩目。然而,对于许多人来说,计算不规则四边形的面积却是一项挑战。你是否也曾为不规则四边形的面积计算而苦恼?是否渴望找到一个简单、通用的公式来解决这一难题?今天,我们就来揭开不规则四边形面积通用公式的神秘面纱,让你轻松掌握这一技能,成为几何计算的高手!

揭开不规则四边形面积通用公式的神秘面纱
在深入探讨不规则四边形面积通用公式之前,我们先来了解一下什么是不规则四边形。不规则四边形,顾名思义,就是四条边长度各不相等、四个角度也各不相同的四边形。与规则的四边形(如正方形、矩形、菱形等)相比,不规则四边形在形状上更加多变,因此在许多实际应用中更为常见。

那么,如何计算不规则四边形的面积呢?传统上,人们认为仅仅知道四条边的长度是无法准确计算出不规则四边形面积的,因为四边形不具有稳定性。然而,随着数学研究的不断深入,我们已经发现了一种新的方法,可以通过已知的四条边长度来估算不规则四边形的面积。

不规则四边形面积通用公式的推导
要理解不规则四边形面积通用公式,我们首先需要了解一个关键概念——中点四边形。中点四边形是由顺次连接任意四边形上的中点所得的四边形,它总是平行四边形。这个性质在推导不规则四边形面积公式时起到了关键作用。

根据数学原理,不规则四边形的面积可以通过以下公式计算:
S = (a + b + c + d) / 2 * sqrt(4a²b² + (c² + d² - a² - b²)² - (c² + d² - a² + b²)²) / (4ab)
其中,S代表不规则四边形的面积,a、b、c、d分别代表四边形的四条边长度。这个公式虽然看起来有些复杂,但只要我们理解了它的推导过程,就能轻松掌握它的应用。
不过,为了方便理解和记忆,我们通常会将这个公式简化为:
S = (a + b + c + d) / 2 * h'
其中,h'是一个与四边形形状有关的参数,它可以通过四边形不相邻两边中点的连线长以及另两边的任一中点到该连线距离的2倍来计算。这个简化公式在实际应用中更加方便快捷。
网格法:直观理解不规则四边形面积
除了上述公式外,我们还可以通过网格法来直观理解不规则四边形的面积。网格法是一种将不规则四边形划分成多个规则的三角形或矩形的方法。通过计算每个规则图形的面积,然后将它们相加,就可以得到不规则四边形的总面积。
具体步骤如下:
1. 划分网格:首先,我们需要将不规则四边形划分成多个规则的三角形或矩形。这一步可以通过在四边形内部绘制对角线或平行线来实现。
2. 计算各部分面积:接下来,我们分别计算每个规则图形的面积。对于三角形,我们可以使用三角形面积公式(面积=1/2×底×高);对于矩形,我们可以使用矩形面积公式(面积=长×宽)。
3. 相加求和:最后,我们将所有规则图形的面积相加,就可以得到不规则四边形的总面积。
虽然网格法需要一些额外的计算步骤,但它提供了一种直观理解不规则四边形面积的方法,有助于我们更好地理解不规则四边形面积通用公式的含义。
直接测量法:适用于特定情况
在某些特定情况下,我们可以直接测量不规则四边形的边长和角度,然后利用四边形面积公式(面积=边长1×边长2×sin(角度))进行计算。这种方法虽然简单直接,但适用范围有限,因为它需要我们知道至少一个角的度数。
然而,在实际应用中,我们往往很难直接测量到不规则四边形的所有边长和角度。因此,直接测量法通常只适用于一些特定情况,如建筑测量、地图制作等领域。
面积定理:巩固几何知识
在探讨不规则四边形面积通用公式的过程中,我们还不得不提到一些重要的面积定理。这些定理不仅有助于我们更深入地理解不规则四边形面积的计算方法,还能巩固我们的几何知识。
1. 一个图形的面积等于它的各部分面积的和:这是面积计算的基本原理之一。它告诉我们,无论图形多么复杂,我们都可以通过将其划分为多个简单图形来计算总面积。
2. 两个全等图形的面积相等:这是面积计算中的一条基本性质。如果两个图形可以完全重合,那么它们的面积一定相等。
3. 等底等高的三角形、平行四边形、梯形(梯形等底应理解为两底的和相等)的面积相等:这条定理告诉我们,在底和高相同的情况下,不同形状的图形可能有相同的面积。
4. 等底(或等高)的三角形、平行四边形、梯形的面积比等于其所对应的高(或底)的比:这条定理进一步扩展了上一条的性质,它告诉我们,在底或高成比例的情况下,不同形状的
- 上一篇: 掌握实心球投掷技巧,让每一次投掷都精准有力!
- 下一篇: 如何在电脑上登录QQ网页版
-
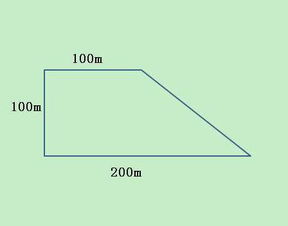 揭秘梯形面积计算的奥秘:一键掌握高效公式新闻资讯12-22
揭秘梯形面积计算的奥秘:一键掌握高效公式新闻资讯12-22 -
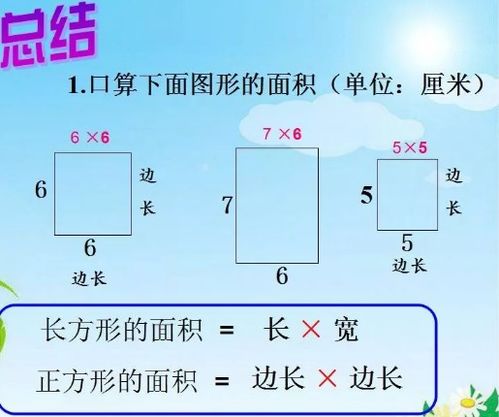 正方形面积计算公式详解新闻资讯10-25
正方形面积计算公式详解新闻资讯10-25 -
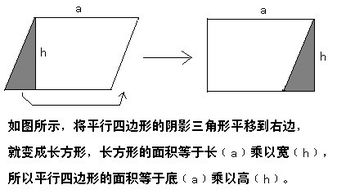 平行四边形面积计算公式详解新闻资讯11-24
平行四边形面积计算公式详解新闻资讯11-24 -
 揭秘!小学生必知的平行四边形面积计算魔法公式新闻资讯11-01
揭秘!小学生必知的平行四边形面积计算魔法公式新闻资讯11-01 -
 揭秘!四边形面积计算公式的全攻略新闻资讯11-01
揭秘!四边形面积计算公式的全攻略新闻资讯11-01 -
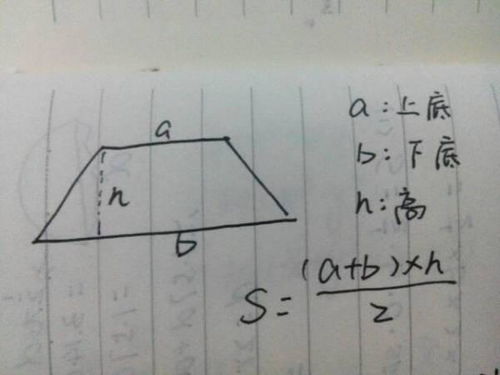 梯形面积计算公式新闻资讯12-02
梯形面积计算公式新闻资讯12-02










