如何定义质因数?有哪些基本特征和例子?
在这个浩瀚的数字宇宙中,你是否曾对那些构建数学大厦的基石——质因数,抱有无限的好奇与遐想?想象一下,每一个正整数,无论大小,都仿佛是由一串串神秘代码编织而成,而解开这些代码的钥匙,正是质因数。今天,就让我们一起踏上一场揭秘之旅,探索“质因数”的神奇世界,感受它在数学与生活中的独特魅力。
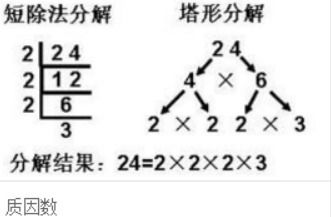
揭秘:质因数的神秘面纱
在数学的广袤天地间,“质因数”一词犹如星辰般璀璨,却又带着几分神秘。简单来说,质因数就是那些只能被1和自己整除的正整数,它们如同构建数字世界的原子,通过不同的排列组合,形成了我们所见的每一个整数。当你尝试将一个正整数拆解成若干个质数相乘的形式时,那些质数就是该数的质因数。
为何质因数如此重要?
或许你会问,质因数究竟有何魔力,让无数数学家和爱好者为之倾倒?答案藏在它的广泛应用与深刻意义之中。
加密与安全的守护者:在信息时代,质因数扮演了加密技术的基石角色。许多高级加密算法,如RSA加密算法,正是基于大质数难以快速分解的原理,确保了数据传输的安全性。没有质因数的保驾护航,我们的网上银行交易、电子邮件通讯可能将暴露在风险之中。
数学之美的展现:质因数的存在,展现了数学中简洁与复杂的完美统一。一个简单的整数背后,可能隐藏着复杂多变的质因数组合,这种内在的逻辑美与秩序感,让数学爱好者们沉醉不已。
问题解决的钥匙:在解决一些数学问题时,质因数分解往往是解题的第一步。从最大公约数、最小公倍数到数论中的许多难题,质因数都是不可或缺的工具。它们像是一把把精密的钥匙,打开了通往答案的大门。
走进质因数的奇妙世界
既然质因数如此重要且迷人,那么我们不妨深入探索一下它的奇妙世界。
质因数的寻找之旅:对于任何给定的正整数,如何找到它的所有质因数?这看似简单的问题背后,其实蕴含着丰富的数学技巧和策略。从试除法到更高级的算法,如轮询筛选法、埃拉托斯特尼筛法等,每一种方法都是人类智慧的结晶。
质因数的独特性质:质因数不仅仅是一堆孤立的数字,它们之间还存在着许多有趣的性质和规律。比如,任何大于1的自然数都可以表示成质数的乘积(算术基本定理);质数在无限大的数集中总是稀疏分布的,但其分布规律至今仍是数学界的一大谜题。
质因数与日常生活的联系:或许你会惊讶地发现,质因数并不只是数学家们的研究对象,它们还悄悄地渗透到了我们的日常生活中。从购物时的找零问题,到设计比赛评分系统时的去重与排序,质因数都在默默地发挥着作用。
结语:质因数——数字世界的秘密钥匙
在这个充满未知与探索的旅程中,我们见证了质因数的非凡魅力与无限可能。它们既是数学大厦的基石,也是信息安全的守护神;它们既展现了数学的简洁与美丽,也揭示了生活中的智慧与奥秘。质因数,这把开启数字世界秘密的钥匙,正等待着每一位热爱数学、勇于探索的你,去发现更多未知的宝藏。
现在,你是否已经对质因数产生了浓厚的兴趣?那么,就让我们携手并进,继续在这条充满挑战与惊喜的数学之路上,探寻更多关于质因数的秘密吧!
- 上一篇: 解析'发小'一词的真正含义
- 下一篇: 揭秘!数学中折扣金额的神奇算法,让你轻松省钱高手
-
 三位数除以一位数的具体例子有哪些新闻资讯11-05
三位数除以一位数的具体例子有哪些新闻资讯11-05 -
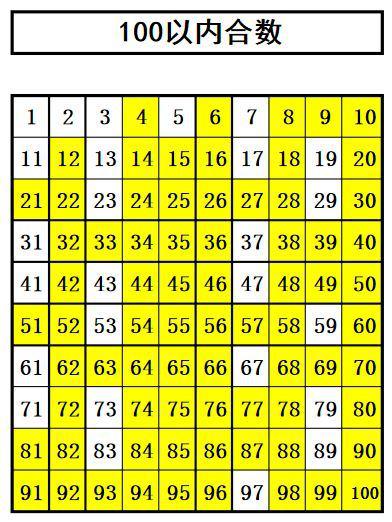 揭秘!你知道哪些数字是神秘的素数吗?新闻资讯10-23
揭秘!你知道哪些数字是神秘的素数吗?新闻资讯10-23 -
 探索因数与倍数的奇妙世界新闻资讯11-08
探索因数与倍数的奇妙世界新闻资讯11-08 -
 如何准确计算功率因数?公式揭秘!新闻资讯12-04
如何准确计算功率因数?公式揭秘!新闻资讯12-04 -
 过渡句定义及实例解析新闻资讯10-31
过渡句定义及实例解析新闻资讯10-31 -
 掌握关键:轻松区分因数与倍数新闻资讯11-10
掌握关键:轻松区分因数与倍数新闻资讯11-10