掌握关键:轻松区分因数与倍数
在数学的世界里,因数和倍数是两个既基础又重要的概念。对于初学者来说,这两个概念往往容易混淆,但通过细致的分析和实例的辅助,我们可以清晰地理解并区分它们。

首先,我们需要明确因数和倍数的定义。因数,指的是能够整除一个给定数的整数。换句话说,如果整数a能够被整数b整除,那么我们就说b是a的一个因数。例如,对于数字12,它的因数有1、2、3、4、6和12。我们可以看到,这些数都能够整除12,不留余数。值得注意的是,一个数的因数总是包括1和它本身。此外,因数还体现了数与数之间的整除关系,这种关系在数学运算和问题解决中经常用到。

倍数,则是相对于一个给定数而言,是这个数的整数倍。也就是说,如果整数a是整数b的c倍(c为整数),那么我们就说a是b的c倍,或者说a是b的倍数。以数字3为例,它的倍数有3、6、9、12等等。这些数都可以表示为3乘以一个整数得到的结果。倍数反映了数与数之间的比例关系,这种关系在日常生活中的计数、测量等方面都有广泛应用。

接下来,我们通过对比和实例进一步区分因数和倍数。

从定义上来看,因数和倍数的主要区别在于它们的“出发点”不同。因数是从被除数(或称为“原数”)出发,寻找能够整除这个数的整数;而倍数则是从原数出发,寻找这个数的整数倍。这种“出发点”的不同导致了它们在数学中的用途和性质上的差异。
在性质上,因数具有“对称性”和“有限性”的特点。对称性指的是,如果b是a的因数,那么a也是b的因数(当然,这里需要排除a和b相等且为质数的情况,因为质数只有两个因数:1和它本身)。例如,2是4的因数,同时4也是2的因数。有限性则指的是,一个数的因数个数是有限的。还是以12为例,它的因数只有1、2、3、4、6和12这六个。
相比之下,倍数则具有“单向性”和“无限性”的特点。单向性指的是,如果a是b的倍数,那么我们不能直接得出b是a的倍数的结论(除非a和b相等)。例如,6是3的倍数,但3不是6的“倍数”(在这个语境下,“倍数”一词通常用于表示较大的数是较小的数的倍数)。无限性则指的是,一个数的倍数个数是无限的。对于任意给定的正整数n,我们都可以找到无数个n的倍数:n、2n、3n、4n……
为了更直观地理解因数和倍数的区别,我们可以通过实例进行说明。
假设我们有一个数字8,我们需要找出它的所有因数和倍数。
首先,我们找出8的所有因数。根据因数的定义,我们需要找到所有能够整除8的整数。通过计算,我们可以得出8的因数有1、2、4和8。这些数都能够整除8,不留余数。
然后,我们找出8的一些倍数。根据倍数的定义,我们需要找到8的整数倍。通过计算,我们可以得出8的倍数有8、16、24、32……等等。这些数都可以表示为8乘以一个整数得到的结果。
通过对比8的因数和倍数,我们可以发现它们的区别:因数是能够整除原数的整数,而倍数是原数的整数倍;因数个数有限,而倍数个数无限;因数具有对称性(除特殊情况外),而倍数具有单向性。
此外,我们还可以利用因数和倍数的性质来解决一些数学问题。例如,判断一个数是否为质数时,我们可以检查它是否只有两个因数:1和它本身。如果一个数除了1和它本身外还有其他因数,那么这个数就不是质数。同样地,在求解最小公倍数和最大公约数等问题时,我们也可以利用倍数和因数的性质来简化计算过程。
最后,需要注意的是,在实际应用中因数和倍数的概念往往与其他数学知识相结合使用。例如,在分数运算中我们需要用到因数来约分和通分;在代数方程中我们需要利用倍数关系来求解未知数;在几何图形中我们也可以通过倍数关系来计算面积和体积等。因此在学习因数和倍数时我们应该将它们与其他数学知识相结合起来理解和掌握。
综上所述,因数和倍数是数学中的两个重要概念它们既相互区别又相互联系。通过明确它们的定义、性质和用途以及结合实例进行说明我们可以更好地理解和掌握这两个概念从而为后续的数学学习和应用打下坚实的基础。
- 上一篇: 舞蹈C位含义解析
- 下一篇: 怎样快速打开支付宝的商家收款二维码?
-
 探索因数与倍数的奇妙世界新闻资讯11-08
探索因数与倍数的奇妙世界新闻资讯11-08 -
 揭秘因数与倍数的奇妙世界新闻资讯11-18
揭秘因数与倍数的奇妙世界新闻资讯11-18 -
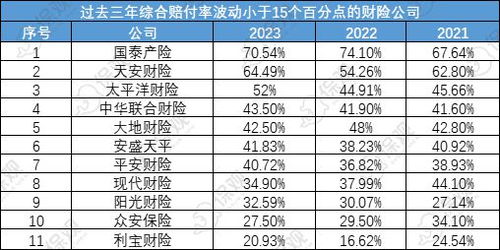 如何计算平赔率与赔付率的具体公式是什么?新闻资讯11-09
如何计算平赔率与赔付率的具体公式是什么?新闻资讯11-09 -
 如何快速求解两个数的最小公倍数?详细步骤揭秘!新闻资讯10-23
如何快速求解两个数的最小公倍数?详细步骤揭秘!新闻资讯10-23 -
 揭秘!1,它究竟是不是质数?新闻资讯10-27
揭秘!1,它究竟是不是质数?新闻资讯10-27 -
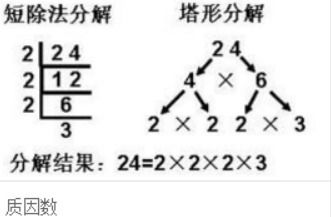 如何定义质因数?有哪些基本特征和例子?新闻资讯10-29
如何定义质因数?有哪些基本特征和例子?新闻资讯10-29












