揭秘!平方计算的奥秘:轻松掌握高效公式与方法
当然,了解“平方”及其计算方法对于数学学习者而言是基础且重要的一环。平方,简而言之,就是一个数自乘的结果。无论你是初学者还是想要复习这一知识点的朋友,接下来我们将直接切入主题,清晰地解释平方的概念、公式以及如何计算。

平方的定义
首先,我们需要明确“平方”的定义。在数学中,一个数的平方就是该数乘以它自己的结果。用数学符号表示,若有一个数$a$,则它的平方写作$a^2$或$a \times a$。平方是一个基础的运算,它在代数、几何、物理等多个领域都有广泛应用。

平方的公式
严格来说,“平方”本身并不涉及复杂的公式,因为它仅仅是一个简单的乘法运算。但如果非要说一个“公式”,那么最直接的就是:

$$ a^2 = a \times a $$

这个公式告诉我们,要求一个数的平方,只需要将这个数乘以它自己即可。例如,求3的平方,就是$3^2 = 3 \times 3 = 9$。
如何计算平方
计算平方的步骤非常简单,按照上面的公式直接操作即可。但这里可以分享一些小技巧,帮助大家更快更准确地完成计算。
1. 直接乘法:对于较小的数,直接相乘是最快的方法。例如,$4^2 = 4 \times 4 = 16$。
2. 利用乘法口诀:特别是小学阶段,很多孩子通过熟记乘法口诀来快速完成平方的计算。这不仅提高了计算速度,也加强了数字敏感度。
3. 观察与拆分:对于较大的数,可以尝试观察它是否能拆分成更简单的部分来计算。虽然这并不总是适用,但在某些情况下能简化计算过程。比如,$25^2$,观察到25是5的平方,因此$25^2 = (5^2)^2 = 5^4 = 625$。
4. 利用计算器:当然,在现代科技的支持下,利用计算器是最便捷的方法。无论是手机还是专用计算器,都能快速给出结果。但要注意的是,不要过分依赖计算器,理解和掌握计算方法才是关键。
5. 特殊数的平方:有一些数的平方具有特殊性质或易于记忆。比如,从1到10的平方($1^2=1, 2^2=4, 3^2=9$...直至$10^2=100$)是基础中的基础,熟练掌握它们对提高计算能力和数学思维能力都有很大帮助。
平方的应用
了解了平方的计算方法后,我们再来看看它在日常生活中的一些应用。
面积计算:在几何学中,平方经常被用来计算二维图形的面积。比如,正方形的面积就是其边长的平方。
物理学中的应用:在物理学中,许多物理量(如速度、加速度、能量等)的计算都涉及到平方。比如,动能$K$的计算公式为$K = \frac{1}{2}mv^2$,其中$m$是质量,$v$是速度,速度的平方体现了速度对动能的影响。
数据分析:在统计学和数据分析中,平方用于计算方差和标准差等指标,这些指标帮助我们判断数据的离散程度。
经济学:在经济学中,复利计算就是一个典型的平方(或更广义地说,是指数)增长模型。在固定利率下,随着时间的推移,投资金额会呈现平方级甚至是指数级的增长。
结语
通过以上内容,我们可以清晰地看到,平方作为一个基础的数学概念,其定义简单、计算方法直接,但在各个领域都有着广泛的应用。无论是学习数学、物理、几何,还是进行数据分析、经济决策,理解和掌握平方的概念及其计算方法都是非常重要的。希望这篇文章能够帮助到你,让你对平方有一个更全面、更深刻的理解。
-
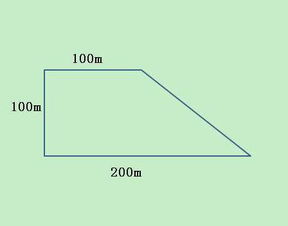 揭秘梯形面积计算的奥秘:一键掌握高效公式新闻资讯12-22
揭秘梯形面积计算的奥秘:一键掌握高效公式新闻资讯12-22 -
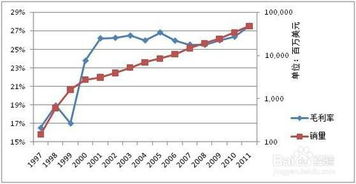 揭秘!轻松掌握毛利率计算公式,让你一眼看穿盈利奥秘新闻资讯10-19
揭秘!轻松掌握毛利率计算公式,让你一眼看穿盈利奥秘新闻资讯10-19 -
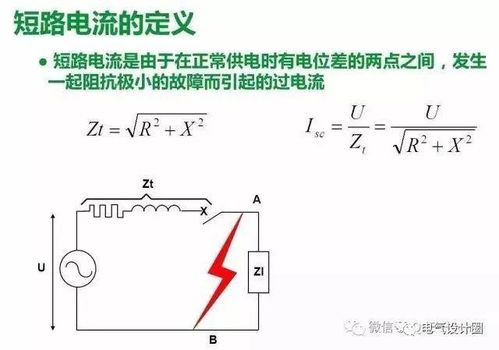 揭秘电流计算的奥秘:轻松掌握计算方法新闻资讯10-31
揭秘电流计算的奥秘:轻松掌握计算方法新闻资讯10-31 -
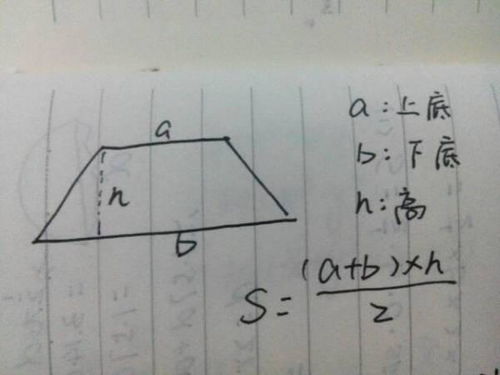 揭秘!梯形面积公式的字母魅力:轻松掌握计算奥秘新闻资讯10-24
揭秘!梯形面积公式的字母魅力:轻松掌握计算奥秘新闻资讯10-24 -
 揭秘!圆形面积计算公式的奥秘,轻松掌握不再难新闻资讯10-19
揭秘!圆形面积计算公式的奥秘,轻松掌握不再难新闻资讯10-19 -
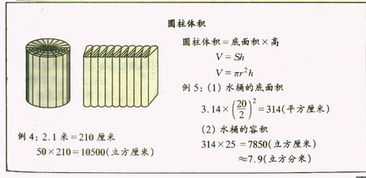 揭秘!圆柱体积计算的神奇公式,轻松掌握空间奥秘新闻资讯10-19
揭秘!圆柱体积计算的神奇公式,轻松掌握空间奥秘新闻资讯10-19












