揭秘!菱形隐藏的神秘性质,你了解多少?
在几何学的广阔天地中,菱形以其独特的形状和丰富的性质,成为了众多图形中一颗璀璨的明珠。不同于一般的平行四边形,菱形以其四边等长的特性,在几何学中占据了特殊的位置。那么,除了这一显著特征外,菱形还具有哪些引人入胜的特殊性质呢?让我们一同深入探索。

对角线性质:相交且垂直平分
首先,菱形的两条对角线不仅是其内在结构的支撑,更是其独特性质的重要体现。在菱形中,两条对角线不仅相互交于一点(即菱形的中心),而且它们还是垂直的,这意味着它们之间的夹角为90度,形成了四个直角三角形。更为奇妙的是,这两条对角线还互相平分对方,即每一条对角线都将另一条对角线分为两段长度相等的部分。这一性质在解决菱形相关问题时,往往能提供关键性的线索和便利。
面积计算:简单高效
提及面积,菱形也展现出了其独特的计算方式。由于菱形的对角线互相垂直且平分,我们可以利用这一性质,通过计算两条对角线长度乘积的一半来轻松求得菱形的面积。这种面积计算方法不仅简洁高效,还体现了菱形对角线性质的深刻应用。
角度关系:邻角互补,对角相等
在菱形中,每一个顶点都是两条相等边的交汇点,这赋予了菱形角度上的独特性质。具体来说,菱形的任意一组邻角都是互补的,即它们的角度之和为180度。同时,菱形的对角也相等,这一性质进一步凸显了菱形结构的对称性。这种角度关系不仅使得菱形在视觉上呈现出和谐的美感,也为菱形在几何证明和计算中提供了有力的依据。
内接圆与外接圆:独特的存在
与其他四边形相比,菱形在圆的关系上也表现出了一定的特殊性。虽然菱形不一定有外接圆(除非它是正方形),但它却一定有一个内接圆,这个圆与菱形的四边都相切。内接圆的存在不仅丰富了菱形的几何结构,还为我们研究菱形与圆的关系提供了新的视角。同时,通过内接圆的性质,我们还可以推导出菱形边长、面积等与其内接圆半径之间的关系,进一步拓展菱形的应用范围。
对称性:中心的对称之美
菱形是一个中心对称图形,这意味着以菱形的中心点为对称中心,菱形上的任意一点关于该中心的对称点都在菱形上。这种中心对称性不仅使菱形在视觉上呈现出一种平衡和谐的美感,还为我们研究和应用菱形提供了极大的便利。例如,在图形变换、图案设计等领域,菱形的中心对称性常常被用作设计元素或变换依据。
旋转与翻折:变换中的稳定性
除了中心对称性外,菱形还具有良好的旋转和翻折稳定性。具体来说,菱形可以围绕其中心点进行任意角度的旋转而保持形状不变;同时,菱形也可以沿着其任意一条对角线进行翻折而得到另一个完全重合的菱形。这种旋转和翻折的稳定性使得菱形在几何变换中具有重要的地位和作用。在实际应用中,我们可以利用菱形的这一性质进行图形的变换、拼接和组合等操作,从而创造出更多富有创意和美感的设计作品。
应用实例:生活中的菱形之美
菱形不仅在数学和几何学中占有重要地位,它在我们的日常生活中也随处可见。从精美的瓷砖图案到时尚的服装设计;从建筑结构的装饰元素到珠宝首饰的设计灵感;菱形以其独特的形状和丰富的性质为我们的生活增添了无限的色彩和美感。同时,菱形在科技、工程、艺术等领域也有着广泛的应用和发挥,它以其独特的魅力和价值赢得了人们的喜爱和追捧。
综上所述,菱形作为几何学中一种特殊的四边形,不仅具有四边等长的显著特征,还在对角线性质、面积计算、角度关系、内接圆与外接圆、对称性、旋转与翻折等方面展现出了丰富的特殊性质。这些性质不仅使得菱形在几何学研究中占有重要地位,也为我们在实际应用中提供了有力的支持和便利。让我们在欣赏菱形之美的同时,也深入挖掘和利用其独特的性质和价值吧!
-
 揭秘!Triangle的真正含义与多样用法,你了解多少?新闻资讯10-21
揭秘!Triangle的真正含义与多样用法,你了解多少?新闻资讯10-21 -
 揭秘!'CMCC'背后隐藏的意义,你了解多少?新闻资讯10-27
揭秘!'CMCC'背后隐藏的意义,你了解多少?新闻资讯10-27 -
 揭秘!火山喷发的神秘过程,你了解多少?新闻资讯10-28
揭秘!火山喷发的神秘过程,你了解多少?新闻资讯10-28 -
 揭秘!茉莉花的神秘花语,你了解多少?新闻资讯10-23
揭秘!茉莉花的神秘花语,你了解多少?新闻资讯10-23 -
 揭秘!你知道哪些数字是神秘的素数吗?新闻资讯10-23
揭秘!你知道哪些数字是神秘的素数吗?新闻资讯10-23 -
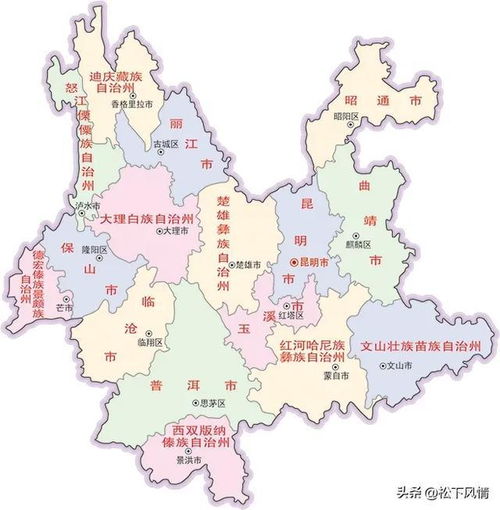 揭秘云南:探寻这片多彩土地上隐藏的地级市瑰宝,究竟有多少座?新闻资讯10-24
揭秘云南:探寻这片多彩土地上隐藏的地级市瑰宝,究竟有多少座?新闻资讯10-24












