分数定义的核心意义与应用解析
在探讨“分数的意义”这一深刻而基础的数学概念时,我们不得不深入其本质,理解它如何在我们的日常生活、学习以及更广阔的科学领域中扮演着不可或缺的角色。分数,这一看似简单的数学符号,实则蕴含了丰富的数学逻辑与实际应用价值,它不仅是数与数之间关系的一种表达,更是人类智慧对连续与离散、部分与整体深刻理解的体现。

分数的起源与基本概念
追溯至远古时期,人类在面对资源分配、测量划分等实际问题时,逐渐意识到单一整数无法满足所有描述需求。于是,分数作为整数之外的一种数的形式应运而生。最初,它可能是以口头或图形的方式存在,如“半个”、“三分之一”等直观描述,随后演变为今天我们所见的分数形式——分子在上,分母在下的标准化表示。这种表示方法不仅简化了复杂的描述,还使分数的运算和比较变得有据可依。

在数学上,分数定义为两个正整数a和b(b≠0)的比值,记作a/b,其中a是分子,表示被除数;b是分母,表示除数。分数表示的是一个整体被分割成b等份后,所取出的a份的大小。这种定义揭示了分数作为“部分与整体关系”的量化工具的本质。

分数的数学意义
1. 数的扩展:分数首先是对自然数(及整数)系统的一种自然扩展。它允许我们表示那些介于两个整数之间的数,从而填补了整数之间的“空隙”,使得数的系统更加完整和连续。

2. 比例与比例尺:分数是描述比例关系的重要工具。无论是地图上的比例尺,还是科学实验中试剂的配比,分数都能精确地表达两个量之间的相对大小关系。
3. 分数运算:分数具有其独特的运算法则,包括加法、减法、乘法和除法。这些运算不仅遵循着与整数运算相似的原则,还涉及到了通分、约分等特有的操作,进一步展现了分数的复杂性和灵活性。
4. 分式与方程:分数是构建分式和方程的基础。在更高层次的数学学习中,分式和方程是解决实际问题的重要工具,而分数则是这些工具的基本组成元素。
分数的实际应用
1. 日常生活:从烹饪时食材的精确配比,到购买商品时的打折计算,分数无处不在。它帮助我们实现资源的合理分配和精确计算,让我们的生活更加有序和高效。
2. 科学研究:在物理、化学、生物学等自然科学领域,分数被广泛应用于描述实验数据、计算反应速率、分析生物种群比例等。它是科学研究中不可或缺的数学工具。
3. 经济金融:在经济学和金融学中,分数(或其小数、百分数形式)用于表示利率、增长率、市场份额等关键经济指标。这些指标不仅影响着企业和个人的经济决策,还对整个社会的经济发展产生深远影响。
4. 教育领域:作为数学教育的重要组成部分,分数的学习不仅培养了学生的逻辑思维和抽象能力,还为他们后续学习更高级的数学知识和解决实际问题打下了坚实的基础。
分数意义的深层次理解
分数不仅仅是一个数学符号或一种数的形式,它更是人类理性思维的结晶。通过对分数的深入理解和运用,我们能够更加精确地把握世界万物的数量关系和变化规律。同时,分数的学习过程也是培养学生数学素养和科学素养的重要途径。它教会我们如何用数学的眼光观察世界、用数学的思维分析问题、用数学的语言表达见解。
总之,分数的意义在于它作为数学体系中的一个重要组成部分,不仅丰富了数的表现形式和运算规则,还为我们认识和改造世界提供了有力的数学工具。通过学习和掌握分数的相关知识,我们能够更好地应对生活中的各种挑战和机遇,为个人的成长和社会的发展贡献自己的力量。
-
 揭秘质量分数的真正含义,一文带你轻松掌握新闻资讯10-30
揭秘质量分数的真正含义,一文带你轻松掌握新闻资讯10-30 -
 分式的定义及实例解析新闻资讯11-23
分式的定义及实例解析新闻资讯11-23 -
 分数求导的奥秘与技巧新闻资讯11-05
分数求导的奥秘与技巧新闻资讯11-05 -
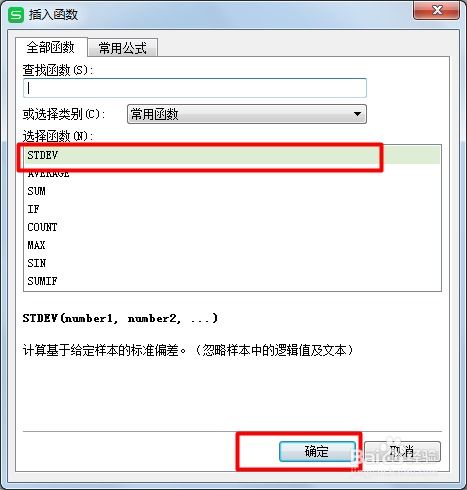 精准掌握:相对偏差计算公式的深度解析新闻资讯11-17
精准掌握:相对偏差计算公式的深度解析新闻资讯11-17 -
 唯物史观与剩余价值学说的定义解析新闻资讯11-10
唯物史观与剩余价值学说的定义解析新闻资讯11-10 -
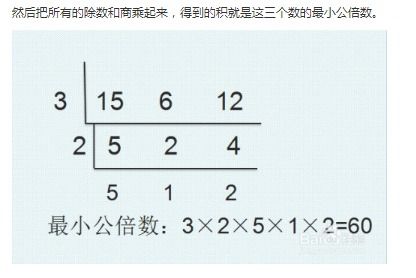 如何计算两个数的最小公倍数?新闻资讯10-22
如何计算两个数的最小公倍数?新闻资讯10-22











