揭秘!长方体体积计算的神奇公式,你知道吗?
在探讨三维空间中的几何体时,长方体作为最基础的立体图形之一,其体积的计算是几何学中的一项基本而重要的内容。长方体,顾名思义,是一个拥有六个矩形面的立体,每对相对的面都完全相同,且三组相对的棱(边)长度分别相等。理解长方体的体积公式,不仅能帮助我们解决日常生活中的实际问题,如计算储物箱、建筑物的某个部分等所需的空间大小,也是深入学习其他复杂几何体体积计算的基础。

长方体的基本特征
首先,简要回顾长方体的基本特征:

六个面:均为矩形,且每对相对的面大小相等。

十二条棱:分为三组,每组四条棱相互平行且等长。这三组棱分别代表了长方体的长、宽、高。

八个顶点:是长方体三条棱的交点。

长方体体积公式的推导
长方体体积的计算基于其三个维度:长(L)、宽(W)、高(H)。为了直观理解这一公式的来源,我们可以采用“切片法”进行推导。
想象一下,如果你有一个长方体形状的蛋糕,并且想要知道它里面包含了多少“小块”蛋糕。一个简单的方法是将这个蛋糕沿着长度方向切成许多等宽的小片,每一小片都是一个矩形(实际上是一个“薄片”的长方体,但其高度非常小,可近似看作二维平面上的矩形)。接下来,计算每一小片的面积(即矩形的面积,等于长乘以宽),然后将所有小片的面积相加,就得到了整个蛋糕的“总面积”(但这里实际上是体积的累积,因为每一小片都有一定的厚度)。由于我们沿着长度方向切片,所以这些小片的宽度和高度都与原长方体相同,唯一变化的是长度被细分成了多段。最终,当我们将所有这些小片的“面积”(实际上是体积,即面积乘以高度)加起来时,就得到了整个长方体的体积。
这个过程可以用数学表达式表示为:每一小片的体积 = L/n × W × H(其中n是切片的数量),而整个长方体的体积则是所有这些小片体积的总和,即当n趋近于无穷大时,这些小片体积之和的极限。但实际上,我们不需要通过极限的方式来计算,因为直接利用乘法原理,长方体的体积可以简单地表示为长、宽、高的乘积:
\[ V = L \times W \times H \]
这就是长方体的体积公式,简洁而直观。
体积公式的应用
掌握了这个公式,我们就可以轻松地解决与长方体体积相关的各种问题。例如:
建筑规划:在建筑设计阶段,需要精确计算不同房间或空间的体积,以确保它们能满足使用需求并符合建筑规范。
包装设计:生产厂商在设计产品包装时,需要考虑包装盒的体积,以确保产品能安全地被放置并有效利用运输空间。
仓储管理:仓库管理人员需要知道存储物品所需的空间大小,以便合理安排货物的存放位置,优化仓库利用率。
注意事项
在使用长方体体积公式时,需要注意以下几点:
确保所有输入值(长、宽、高)都是正数,因为体积是一个描述物体占据空间大小的量,不能为负。
单位一致性:在计算过程中,所有维度(长、宽、高)的单位必须保持一致,否则会得到错误的结果。例如,如果长度以米为单位,宽度和高度也应以米为单位。
特殊情况处理:对于特殊形状的长方体,如长度、宽度或高度中的某一值为零,那么该长方体的体积将为零,因为它不占据任何实际的空间。
结语
长方体的体积公式是三维几何学中一个基础且极其重要的概念,它不仅具有广泛的应用价值,而且是进一步学习更复杂几何体体积计算的基础。通过理解长方体体积公式的推导过程和应用场景,我们可以更加深入地把握三维空间中的几何关系,为解决实际问题提供有力的数学工具。希望本文的介绍能够帮助您更好地理解和应用长方体的体积公式。
- 上一篇: 掌握台球技巧,轻松打出精彩一杆!
- 下一篇: 解锁百度畅听版新技能:轻松一步,开启识万物神奇之旅!
-
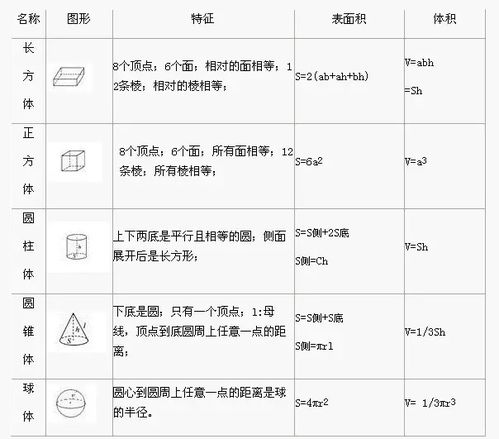 Q&A解锁:长方形与正方形,面积、体积、表面积公式大揭秘,你知道多少?新闻资讯10-25
Q&A解锁:长方形与正方形,面积、体积、表面积公式大揭秘,你知道多少?新闻资讯10-25 -
 长方体的体积计算公式是什么?一键揭秘!新闻资讯10-27
长方体的体积计算公式是什么?一键揭秘!新闻资讯10-27 -
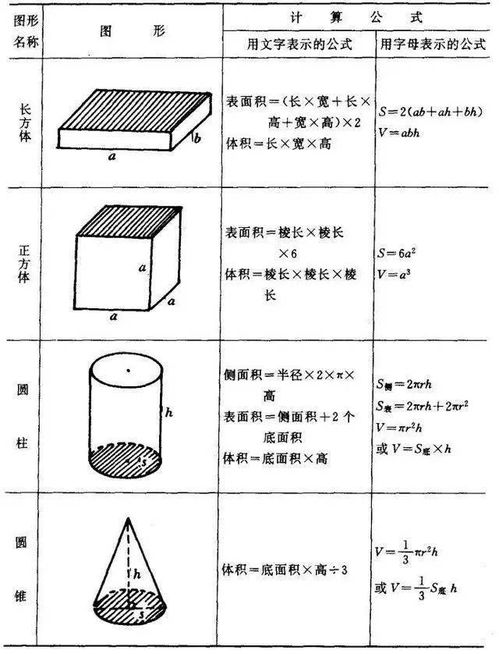 揭秘!长方体体积计算公式全解析新闻资讯10-27
揭秘!长方体体积计算公式全解析新闻资讯10-27 -
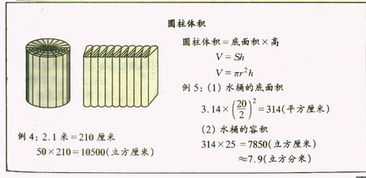 揭秘!圆柱体积计算的神奇公式,轻松掌握空间奥秘新闻资讯10-19
揭秘!圆柱体积计算的神奇公式,轻松掌握空间奥秘新闻资讯10-19 -
 圆锥体积的计算公式是什么新闻资讯11-22
圆锥体积的计算公式是什么新闻资讯11-22 -
 如何计算正方形的体积新闻资讯11-02
如何计算正方形的体积新闻资讯11-02












