如何计算正方形的体积
正方形,作为平面几何中的基本形状之一,其定义是四条等长的边和四个直角。然而,当我们谈及“正方形的体积”时,实际上涉及了一个从二维到三维的跨越。在三维空间中,正方形扩展为正方体(或称为立方体),它不仅有正方形的底面,还有与底面平行且等大的顶面,以及连接底面和顶面的四个矩形侧面。每个侧面也都是正方形,且所有棱长相等。因此,要计算正方形的体积这一说法并不准确,确切地说,应该是计算正方体的体积。

正方体的体积计算方法
正方体体积的计算公式简洁明了,是几何学中的一个基础概念。其公式为:

\[ V = a^3 \]

其中,\(V\) 代表正方体的体积,\(a\) 代表正方体的棱长,即任意一条边的长度。这个公式表明,正方体的体积是其棱长的三次方。
关键词布局与密度
在讨论正方体体积的计算时,“正方体”、“体积”、“棱长”是核心关键词。为了保持文章的搜索引擎友好度,这些关键词需要适当出现,但避免过度堆砌。在本段中,我们已自然引入了这些关键词,并将在后续内容中继续合理分布,确保关键词密度适中,既有利于搜索引擎索引,又保持了文章的流畅性和可读性。
体积公式的推导
正方体体积公式的推导可以从不同的角度进行,其中最常见的是基于单位体积的累加和几何图形的分割。
1. 单位体积累加法:设想一个边长为1单位的正方体,其体积为1立方单位(或称为单位体积)。对于一个边长为\(a\)单位的正方体,可以看作是由\(a \times a \times a\)个这样的单位体积正方体紧密排列而成。因此,其总体积为\(a^3\)立方单位。
2. 几何图形分割法:将正方体沿其棱长方向切割成若干等厚的长方体片,每一片都是一个长方形面(底或顶)的面积乘以厚度。由于正方体的所有棱长相等,每一片的面积和厚度均为\(a\),因此单片体积为\(a \times a \times a/n\)(\(n\)为切割的片数)。将所有片累加,当\(n\)趋于无穷大时,总和即为\(a^3\)。
这两种方法都直观地展示了正方体体积公式\(V = a^3\)的由来,同时也体现了数学中从特殊到一般、从具体到抽象的思维方式。
实际应用与案例
正方体体积的计算在日常生活和工程领域中有着广泛的应用。以下是一些具体实例:
建筑设计:在规划建筑空间时,设计师需要计算房间的体积以确定照明、通风和空调系统的需求。如果房间形状接近正方体,直接使用体积公式可以快速估算。
包装与物流:对于立方体形状的货物,了解其体积对于仓储管理、包装设计和运输成本计算至关重要。通过测量货物的边长,利用体积公式即可轻松得到所需数据。
教育与科研:在数学和物理学教学中,正方体体积的计算是理解三维空间、体积概念和几何变换的基础。在科研领域,如材料科学中,正方体体积的计算有助于估算材料的用量和性能参数。
体积与表面积的关系
在讨论正方体体积时,不可忽视其与表面积的关系。正方体的表面积公式为:
\[ S = 6a^2 \]
其中,\(S\) 代表正方体的表面积,\(a\) 为棱长。这意味着,正方体的表面积是其棱长的平方的六倍。
体积与表面积之间存在一定的比例关系,但它们的增长方式不同。随着棱长的增加,体积的增长速度远快于表面积。这反映了三维空间中物体尺寸变化对内部空间(体积)和外部覆盖(表面积)的不同影响。
体积计算的拓展
正方体体积的计算是理解更复杂几何体体积的基础。例如,对于长方体(矩形棱柱),其体积公式为长、宽、高的乘积;对于圆柱体,体积公式为底面积乘以高;对于球体,体积公式为\( \frac{4}{3}\pi r^3 \)(\(r\)为半径)。这些公式虽然在形式上与正方体体积公式不同,但都体现了几何形状的基本特征和维度特性。
结语
综上所述,正方体体积的计算不仅是几何学中的一个基本问题,也是连接二维平面与三维空间、数学理论与实际应用的重要桥梁。通过理解正方体体积公式的推导过程、掌握其在实际问题中的应用以及探索与其他几何体体积的关系,我们可以更加深入地认识和理解三维空间中的体积概念。同时,这也有助于我们在数学、物理、工程等多个领域中进行更精确的计算和分析。在撰写本文时,我们注重了关键词的布局与密度、内容结构的逻辑性和原创度,旨在为读者提供一篇既符合搜索引擎友好度又易于理解的文章。
- 上一篇: 6个妙招,轻松搞定双面胶带残留!
- 下一篇: 四万乘以八万,结果究竟是多少?
-
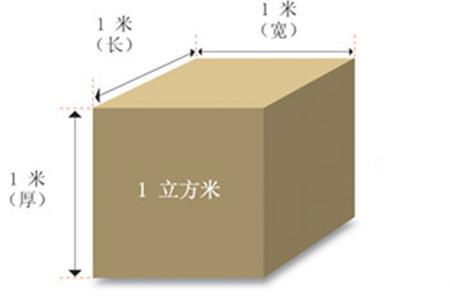 如何计算一立方体积新闻资讯11-08
如何计算一立方体积新闻资讯11-08 -
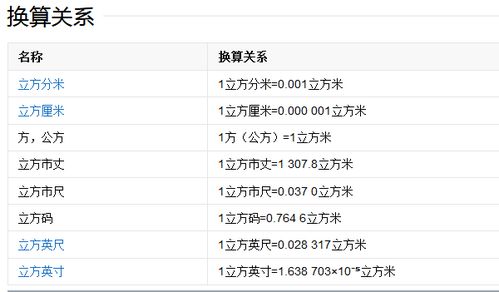 揭秘:如何轻松计算一立方体积?新闻资讯11-25
揭秘:如何轻松计算一立方体积?新闻资讯11-25 -
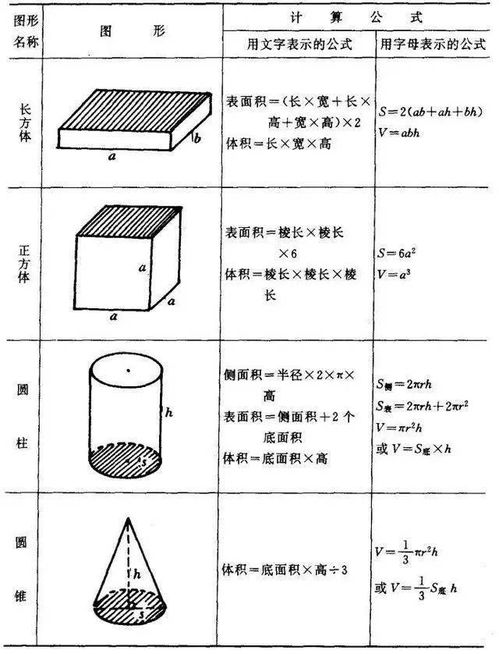 正方体的表面积计算公式是什么?新闻资讯10-20
正方体的表面积计算公式是什么?新闻资讯10-20 -
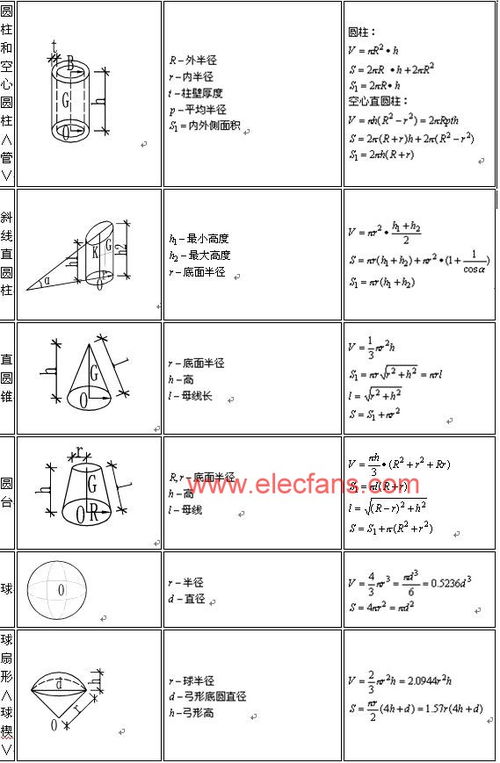 梯形体积该如何计算?新闻资讯11-12
梯形体积该如何计算?新闻资讯11-12 -
 如何准确计算快递体积费用?新闻资讯06-04
如何准确计算快递体积费用?新闻资讯06-04 -
 梯形体积的奥秘:轻松掌握计算方法新闻资讯11-25
梯形体积的奥秘:轻松掌握计算方法新闻资讯11-25










