轻松学会求几何平均值的方法
在探索数学与统计学的奥秘中,有一个既实用又迷人的概念——几何平均值。它不同于我们日常熟悉的算术平均值,却在众多领域如金融分析、工程设计和生物学研究中发挥着至关重要的作用。想象一下,你正在评估一组投资回报率,或是计算一系列尺寸的平均值以确保产品设计的合理性,这时,几何平均值就成了你的得力助手。本文将带你深入了解如何求解几何平均值,揭秘其背后的原理,并通过实例展示其实际应用,让你轻松掌握这一数学利器。

一、揭开几何平均值的神秘面纱
几何平均值,简而言之,就是一组数的乘积的n次方根,其中n是这组数的个数。与算术平均值(所有数相加后除以数的个数)相比,几何平均值更重视数的相对大小,特别是在处理具有乘法效应的数据时。比如,考虑两个投资项目的年收益率分别为50%和-50%,算术平均值为0%,但显然,连续经历这样的收益率后,你的本金将大幅缩水,这时几何平均值就能更准确地反映实际情况。

二、几何平均值的计算公式
要计算几何平均值,首先需要掌握其基本公式。假设有一组数A1, A2, ..., An,其几何平均值G的计算公式为:

G = (A1 * A2 * ... * An)^(1/n)

这个公式告诉我们,要找到几何平均值,只需将这组数的乘积取n次方根即可。需要注意的是,所有数必须为正数,因为负数或零的乘积会导致无法定义的结果。
三、几何平均值的求解步骤
步骤一:确定数据集合
首先,明确你要计算几何平均值的数据集合。这些数据应该是正数,且数量n至少为2。
步骤二:计算乘积
接下来,将集合中的所有数相乘,得到一个乘积值。
步骤三:取n次方根
最后,将乘积值取n次方根,即可得到这组数的几何平均值。
四、几何平均值的性质与特点
乘法性质:几何平均值特别适用于具有乘法关系的数据,如增长率、比率和倍数。
敏感性:与算术平均值相比,几何平均值对极端值更为敏感,一个很小的数或一个很大的数都会显著影响最终结果。
不变性:当一组数中每个数都乘以或除以同一个正数时,其几何平均值也会相应地乘以或除以该数,但相对比例保持不变。
五、几何平均值的实际应用
金融领域
在金融领域,几何平均值常用于计算投资组合的平均年化收益率,特别是当收益率在不同期间波动较大时。它能帮助投资者更准确地评估长期投资绩效,避免被短期的高收益率所迷惑。
工程设计
在工程设计中,几何平均值用于确定一组尺寸或参数的平均值,以确保设计的兼容性和效率。例如,在设计管道系统时,可能需要计算不同管径的平均值,以确保流体流动顺畅且压力损失最小。
生物学与医学
在生物学和医学研究中,几何平均值用于分析生物体的生长速率、种群密度等具有乘法效应的数据。它有助于科学家更好地理解生物系统的动态变化。
经济学
在经济学中,几何平均值用于计算消费者价格指数(CPI)的平均增长率,以及分析通货膨胀率等经济指标。它提供了对经济趋势的更准确反映。
六、实例演示:计算几何平均值
假设我们有一组投资项目的年收益率数据:[120%, 80%, 150%, 90%]。首先,将这些收益率转换为小数形式:[1.2, 0.8, 1.5, 0.9]。然后,计算这些数的乘积:1.2 * 0.8 * 1.5 * 0.9 = 1.296。最后,取这个乘积的4次方根,得到几何平均值约为1.09。这意味着,从长期角度看,这组投资项目的平均年化收益率约为9%。
七、几何平均值与算术平均值的比较
虽然几何平均值和算术平均值都是衡量一组数中心趋势的指标,但它们在不同情境下各有优势。算术平均值易于计算和理解,适用于大多数日常情况;而几何平均值则更适合处理具有乘法效应的数据,特别是在金融、工程学和生物学等领域。
八、总结
几何平均值作为一种重要的数学工具,不仅在数学和统计学中占有一席之地,更在多个领域发挥着不可替代的作用。通过掌握其计算方法和应用原理,我们能够更深入地理解数据的本质特征,做出更明智的决策。无论是评估投资组合的绩效、设计高效的工程系统,还是研究生物系统的动态变化,几何平均值都是一把不可或缺的钥匙。现在,你已经掌握了求解几何平均值的秘诀,是时候用它来解锁数据背后的秘密了!
- 上一篇: 轻松学会:如何设置手机个性背景壁纸
- 下一篇: 王蓝莓的幸福生活3:解锁养宠物三朵小红花秘籍
-
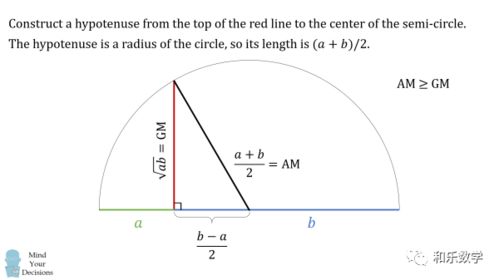 几何平均值如何表示?新闻资讯11-12
几何平均值如何表示?新闻资讯11-12 -
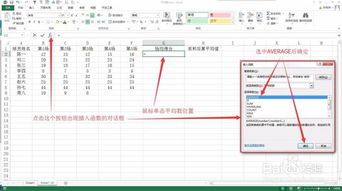 Excel计算平均数的三大高效技巧新闻资讯11-10
Excel计算平均数的三大高效技巧新闻资讯11-10 -
 算术平均数与几何平均数:揭开它们之间的神秘面纱新闻资讯11-12
算术平均数与几何平均数:揭开它们之间的神秘面纱新闻资讯11-12 -
 轻松掌握:如何在条形统计图中求中位数新闻资讯10-27
轻松掌握:如何在条形统计图中求中位数新闻资讯10-27 -
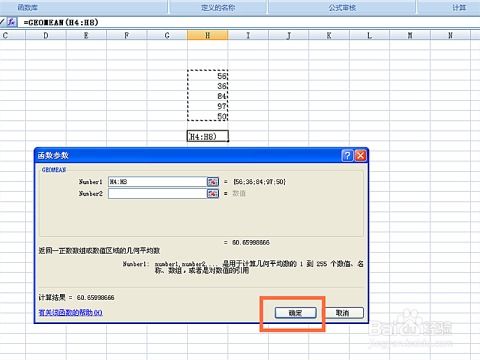 如何轻松掌握Excel函数?揭秘GEOMEAN函数的高效用法新闻资讯12-02
如何轻松掌握Excel函数?揭秘GEOMEAN函数的高效用法新闻资讯12-02 -
 轻松掌握复数求模技巧新闻资讯11-23
轻松掌握复数求模技巧新闻资讯11-23










