轻松掌握:如何在条形统计图中求中位数
在探讨如何在条形统计图中寻找中位数时,我们首先需要明确几个核心概念:条形统计图、数据集合以及中位数。条形统计图是一种直观展示各类别数据数量的图表形式,每个条形的长度代表对应类别的数据数量或频数。中位数,则是将数据从小到大排序后,位于中间位置的数,如果数据量是奇数,则中位数就是正中间的数;如果数据量是偶数,则中位数是中间两个数的平均值。

如何在条形统计图中估算中位数
虽然条形统计图直接给出了各类别的数量,但并不直接展示数据点的具体值或完整的排序,因此直接“找出”中位数并不像在数值列表中那样直接。不过,我们可以通过几个步骤来估算中位数。

步骤一:理解数据结构
首先,观察条形统计图,理解它所代表的数据集结构。注意各个条形的长度(即各类别的数量)以及它们之间的关系。

步骤二:数据总数估算
接下来,估算整个数据集的总数。这可以通过将所有条形的长度(即各类别的数量)相加来实现。如果条形统计图已经给出了总数,这一步将更为直接。
步骤三:确定数据的中点位置
有了数据总数后,我们需要找到这个总数的中点。如果总数是奇数,则中点即为中位数所在的位置(在排序后的数据中);如果总数是偶数,则中位数位于两个中间数的位置之间。
步骤四:估算中位数
1. 如果总数是奇数:
假设数据总数为N(N为奇数),那么中位数就是排序后位于(N+1)/2位置的数。
在条形统计图中,虽然不能直接看到每个具体的数据点,但可以根据各类别的数量分布来估算。观察哪个类别或哪几个类别加起来的数量接近或刚好达到总数的一半,尤其是要注意那些长度较长的条形。
如果某个条形的数量直接就是总数的一半,那么这个类别的代表值(或该类别内数据的中间值,如果知道的话)很可能就是中位数。
如果不是,则需要结合多个类别的数量,特别是那些数量接近总数一半的类别,来估算中位数的可能值。
2. 如果总数是偶数:
假设数据总数为N(N为偶数),那么中位数是两个中间数的平均值,即位于N/2和N/2+1位置的数。
同样地,通过观察条形统计图,找到那些数量累计接近总数一半的两个类别。这两个类别的代表值(或它们内部数据的中间值)将帮助我们估算中位数。
如果两个类别的数量总和刚好是总数的一半,那么这两个类别内数据的平均中间值可能是中位数的一个良好估计。
如果不是,可能需要更复杂的估算,比如考虑这两个类别之间(或之前/之后)的其他类别数据分布,来更精确地估算中位数。
注意事项
估算过程中应意识到,由于条形统计图并不提供数据点的具体值或完整排序,因此得到的中位数只是一个估计值,可能存在一定的误差。
如果数据集中存在极端值(即远离大多数数据点的值),这些值可能会对中位数产生显著影响,但在条形统计图中,这些极端值的影响可能不那么直观。
如果可能的话,获取原始数据集或至少更多关于数据集分布的信息,将有助于更准确地估算中位数。
通过以上步骤,我们可以在不直接看到数据点具体值的情况下,利用条形统计图提供的信息来估算数据集的中位数。这种能力对于数据分析、统计理解和数据可视化解读都是非常重要的。
- 上一篇: 笼字的正确拼音怎么读?一秒学会,轻松掌握!
- 下一篇: 中通快递订单状态实时查询
-
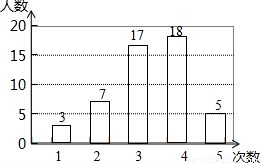 数学统计图:深入解析众数、平均数、中位数的计算方法与应用新闻资讯10-27
数学统计图:深入解析众数、平均数、中位数的计算方法与应用新闻资讯10-27 -
 制作统计图的方法与技巧新闻资讯12-05
制作统计图的方法与技巧新闻资讯12-05 -
 打造条形统计图的秘籍:步骤口诀大揭秘新闻资讯11-26
打造条形统计图的秘籍:步骤口诀大揭秘新闻资讯11-26 -
 轻松掌握:如何快速求解中位数新闻资讯10-27
轻松掌握:如何快速求解中位数新闻资讯10-27 -
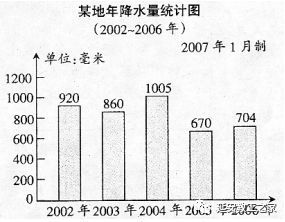 条形统计图和折线统计图各有哪些优点?新闻资讯11-09
条形统计图和折线统计图各有哪些优点?新闻资讯11-09 -
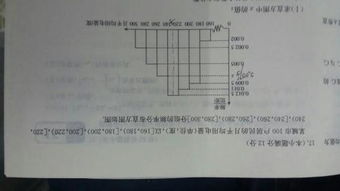 如何计算频率分布直方图的中位数?公式及应用详解新闻资讯10-27
如何计算频率分布直方图的中位数?公式及应用详解新闻资讯10-27












