正弦函数图像是如何绘制的?
揭秘正弦函数图像的绘制奥秘:从数学原理到生动呈现

在数学的浩瀚宇宙中,正弦函数如同一颗璀璨的星辰,以其独特的周期性和波动性,在众多科学领域中发挥着不可替代的作用。你是否曾好奇,那些精美的正弦函数图像究竟是如何绘制出来的?今天,就让我们一起揭开这个神秘的面纱,从数学原理出发,探索正弦函数图像的绘制全过程,并欣赏其在现实生活中的广泛应用。

一、正弦函数:波动的数学之美

正弦函数,一个看似简单的数学表达式y=sin(x),却蕴含着无尽的奥秘。在数学上,正弦函数表示的是一个角度x(以弧度为单位)的正弦值y。它在一个完整的周期内,从0开始,先增后减,再回到0,形成一个完美的波浪形曲线。这个周期性的波动,使得正弦函数在物理学、工程学、信号处理等众多领域中都扮演着重要角色。
二、绘制基础:坐标系与角度转换
要绘制正弦函数图像,首先需要一个坐标系。在二维平面上,我们习惯使用直角坐标系,即x轴和y轴垂直相交的平面。正弦函数的x轴通常表示角度(以弧度为单位),而y轴则表示该角度的正弦值。
接下来,我们需要将角度转换为弧度。在数学中,角度和弧度是可以相互转换的,而正弦函数通常使用弧度制进行计算。例如,一个完整的圆周角度为360度,转换为弧度则为2π。因此,在绘制正弦函数图像时,我们需要将x轴上的每一个点都视为一个弧度值。
三、绘制步骤:从点到线
1. 确定周期:正弦函数的周期T是2π,这意味着函数在一个完整的周期内会重复其波形。因此,在绘制图像时,我们通常选择[-π, π]或[0, 2π]作为x轴的取值范围。
2. 计算正弦值:对于x轴上的每一个点x,我们都需要计算其对应的正弦值y=sin(x)。这可以通过计算器、数学软件或编程实现。
3. 绘制点:在坐标系中,我们根据计算出的(x, y)值,绘制出对应的点。这些点将构成正弦函数图像的轮廓。
4. 连接点:最后,我们使用平滑的曲线将这些点连接起来,形成正弦函数的波形。在绘制时,要注意保持曲线的平滑性和连续性,以准确反映正弦函数的周期性波动。
四、优化技巧:让图像更生动
1. 调整比例尺:根据正弦函数的波动范围,我们可以调整坐标系的比例尺,使图像更加清晰和易于理解。例如,如果正弦函数的波动范围较小,我们可以适当缩小y轴的比例尺,以便更详细地观察其波形。
2. 添加网格线:在坐标系中添加网格线可以帮助我们更准确地定位点和连接曲线。同时,网格线还能增强图像的视觉效果,使其更加美观和易于阅读。
3. 使用颜色和高亮:为了突出正弦函数的波形,我们可以使用不同的颜色和高亮效果来强调其关键特征。例如,可以使用鲜艳的颜色来绘制正弦函数的波形曲线,并使用不同的颜色或阴影来表示其周期性和对称性。
4. 标注关键信息:在图像上标注关键信息,如周期、振幅、相位等,可以帮助我们更好地理解正弦函数的性质和特点。这些信息不仅可以作为图像的补充说明,还能在后续的分析和计算中发挥重要作用。
五、现实应用:正弦函数图像的广泛影响
正弦函数图像的绘制不仅是一门数学技巧,更是一种科学探索的过程。它在现实生活中有着广泛的应用和影响。
1. 物理学:在物理学中,正弦函数被广泛应用于描述波动现象,如声波、光波和电磁波等。通过绘制正弦函数图像,我们可以直观地观察和理解这些波动现象的传播规律和特点。
2. 工程学:在工程学中,正弦函数被用于设计机械振动系统、控制系统和信号处理系统等。通过绘制正弦函数图像,我们可以分析系统的稳定性和性能,并进行优化和改进。
3. 音乐与音频:在音乐和音频领域,正弦函数被用于描述声音的波形和频谱。通过绘制正弦函数图像,我们可以分析声音的频率、振幅和相位等参数,从而进行音频处理、合成和编辑等工作。
4. 电子与通信:在电子与通信领域,正弦函数被用于描述信号的传输和处理过程。通过绘制正弦函数图像,我们可以观察和分析信号的波形、频率和相位等特征,从而实现信号的接收、解码和传输等功能。
六、结语:探索不止,发现无限
正弦函数图像的绘制是一个充满挑战和乐趣的过程。它不仅需要我们掌握扎实的数学知识和技巧,还需要我们具备创新思维和探索精神。通过不断学习和实践,我们可以发现正弦函数图像的更多奥秘和可能性,并将其应用于更广泛的领域和场景中。
在这个过程中,我们不仅要关注正弦函数本身的性质和特点,还要关注其与现实世界的联系和影响。通过深入探索和实践,我们可以更好地理解正弦函数图像的科学价值和现实意义,为人类社会的发展和进步贡献自己的力量。
总之,正弦函数图像的绘制是一门既古老又年轻的科学。它既是数学原理的生动体现,也是科学探索的无限延伸。让我们携手共进,在探索正弦函数图像的奥秘中发现更多惊喜和可能!
- 上一篇: 微信年度账单大揭秘:一键查询你的消费足迹
- 下一篇: 如何准确计算功率因数?公式揭秘!
-
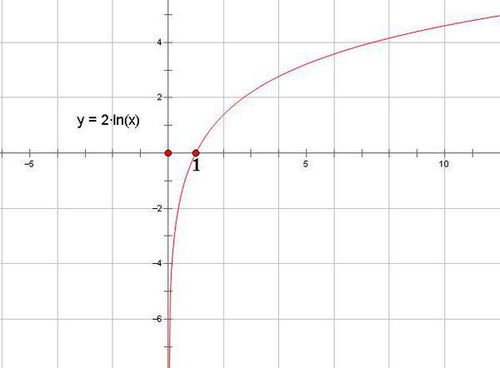 如何绘制lnx绝对值的清晰图像教程新闻资讯10-21
如何绘制lnx绝对值的清晰图像教程新闻资讯10-21 -
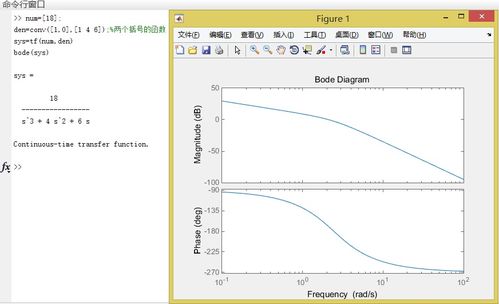 MATLAB技巧:利用IOTransfer与du2y函数绘制Impulse响应图详解新闻资讯04-02
MATLAB技巧:利用IOTransfer与du2y函数绘制Impulse响应图详解新闻资讯04-02 -
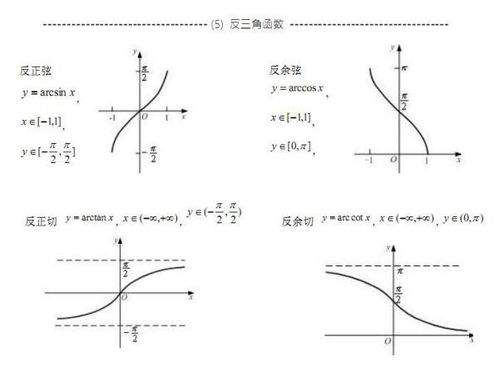 arc三角函数的导数分别是什么?新闻资讯11-22
arc三角函数的导数分别是什么?新闻资讯11-22 -
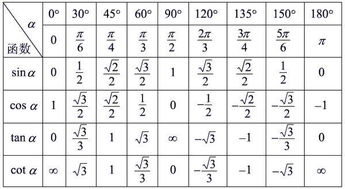 揭秘三角函数值:全面掌握角度与比值的奥秘新闻资讯11-04
揭秘三角函数值:全面掌握角度与比值的奥秘新闻资讯11-04 -
 正弦定理和余弦定理分别是什么?新闻资讯11-09
正弦定理和余弦定理分别是什么?新闻资讯11-09 -
 用函数画图宝绘制指数函数图像的方法新闻资讯10-27
用函数画图宝绘制指数函数图像的方法新闻资讯10-27








