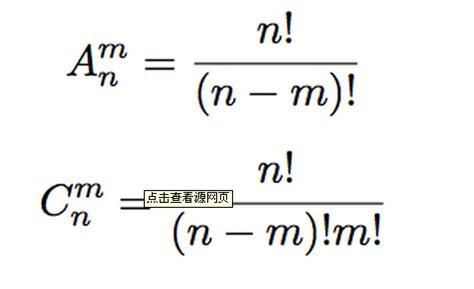组合计算公式的详细解析
组合计算公式是数学中的一个基本概念,广泛应用于统计学、概率论、计算机科学等多个领域。简单来说,组合是从n个不同元素中,不考虑顺序地取出m个元素的所有取法。这种不考虑顺序的选取方式,使得组合与排列(排列需要考虑顺序)有所不同。

组合计算的基本公式是C(n, m),读作“n选m”,表示从n个不同元素中取出m个元素的组合数。具体的计算公式为:
C(n, m) = n! / (m!(n-m)!)
其中,n!表示n的阶乘,即n×(n-1)×...×2×1,特别地,0! = 1。这个公式揭示了组合数的计算方法,即通过计算n个元素的全部排列数,然后除以m个元素的排列数和(n-m)个元素的排列数的乘积,来得到不考虑顺序的组合数。
为了更好地理解组合计算公式,我们可以通过一些具体的例子来阐述。
假设我们有一个包含5个元素的集合A = {1, 2, 3, 4, 5},我们想要从中选出2个元素的所有组合。根据组合计算公式,我们有:
C(5, 2) = 5! / (2!3!) = (5×4×3×2×1) / ((2×1)×(3×2×1)) = 10
因此,从集合A中选出2个元素的所有组合共有10种,分别是(1,2)、(1,3)、(1,4)、(1,5)、(2,3)、(2,4)、(2,5)、(3,4)、(3,5)和(4,5)。
组合计算公式的一个重要性质是互补性质,即C(n, m) = C(n, n-m)。这意味着,从n个元素中选出m个元素的组合数与从n个元素中选出(n-m)个元素的组合数是相同的。例如,从5个元素中选出2个元素的组合数与从5个元素中选出3个元素的组合数都是10。
组合计算公式在实际应用中具有广泛的应用。在统计学中,组合数可以用于计算样本空间的大小,例如在无放回抽样中,从n个元素中抽取m个元素的样本空间大小就是C(n, m)。在概率论中,组合数可以用于计算某些事件的概率,例如,在一个装有n个不同颜色球的袋子中随机取出m个球,求取出某种颜色球的组合方式的概率。在计算机科学中,组合数可以用于计算算法的复杂度,例如在穷举搜索算法中,需要计算所有可能的组合数来确定算法的运行时间。
此外,组合计算公式还可以与其他数学工具相结合,用于解决更复杂的问题。例如,在生成函数理论中,组合数可以用于构建生成函数,从而解决组合计数问题。在线性代数中,组合数可以用于计算矩阵的行列式,进而解决线性方程组的解的问题。在组合优化中,组合数可以用于评估算法的性能,例如,在旅行商问题中,需要计算所有可能的城市组合,以确定最短路径。
值得注意的是,虽然组合计算公式在理论上可以应用于任何正整数n和m,但在实际应用中,当n和m的值非常大时,计算组合数可能会变得非常复杂和耗时。因此,在实际应用中,通常采用一些近似算法或数值方法来计算组合数,以提高计算效率。
除了基本的组合计算公式外,还有一些相关的组合数学概念和公式,如二项式定理、斯特林公式等。二项式定理给出了(a+b)^n的展开式中各项系数的计算方法,其中就涉及到了组合数。斯特林公式则是一种近似计算阶乘的方法,可以用于计算组合数的近似值。
总的来说,组合计算公式是数学中一个重要的工具,具有广泛的应用价值。通过理解和掌握组合计算公式,我们可以更好地解决各种实际问题,提高数学素养和计算能力。
在实际应用中,我们还需要注意一些与组合计算公式相关的概念和方法。例如,重复组合是指从n个不同元素中,不考虑顺序地取出m个元素的所有取法,但允许选取的元素重复。重复组合的计算公式为C(n+m-1, m),这与基本的组合计算公式有所不同。此外,还需要注意组合数的性质,如互补性质、递增性质等,这些性质在解决实际问题时具有重要的应用价值。
总之,组合计算公式是数学中一个重要的基本概念和工具。通过深入理解和掌握组合计算公式及其相关概念和方法,我们可以更好地应用数学知识和方法来解决各种实际问题,提高数学素养和计算能力。同时,我们也需要不断探索和实践,将组合计算公式与其他数学工具相结合,以应对更复杂和更实际的数学问题。
- 上一篇: 如何在百度地图中查看热力图
- 下一篇: 如何查询国开大学的学号?
-
 组合计算公式的定义及应用新闻资讯11-04
组合计算公式的定义及应用新闻资讯11-04 -
 如何轻松计算同比增长率(详细公式解析)新闻资讯11-13
如何轻松计算同比增长率(详细公式解析)新闻资讯11-13 -
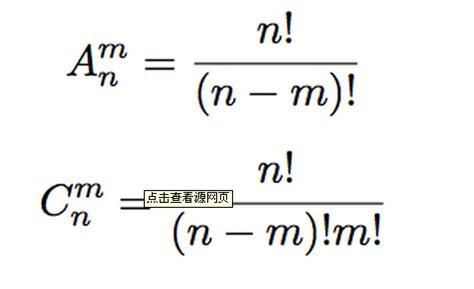 CNM排列组合公式详解新闻资讯11-23
CNM排列组合公式详解新闻资讯11-23 -
 揭秘:概率计算公式全解析新闻资讯10-25
揭秘:概率计算公式全解析新闻资讯10-25 -
 揭秘:频率计算公式的详细解析新闻资讯11-23
揭秘:频率计算公式的详细解析新闻资讯11-23 -
 揭秘:重量计算公式全解析新闻资讯11-13
揭秘:重量计算公式全解析新闻资讯11-13