揭秘:频率计算公式的详细解析
在我们日常生活和科学研究中,频率是一个非常重要的概念。频率描述了在一定时间内某个事件发生的次数,比如在音乐中,音符振动的快慢决定了音调的高低;在无线通信中,信号的频率决定了数据传输的方式和质量。那么,频率是如何计算的呢?今天,我们就来详细聊聊频率计算公式的各个方面,让即便是非专业人士也能轻松理解。

一、频率的基本概念
频率(Frequency)通常用字母f表示,是单位时间内某一事件发生的次数。在国际单位制(SI)中,频率的单位是赫兹(Hz),1赫兹等于每秒1次。因此,如果某个事件每秒发生5次,其频率就是5赫兹。
为了更好地理解频率,我们可以想象一个简单的场景:钟摆。假设你有一个准确的钟表,里面的钟摆每秒摆动一次,那么这个钟摆的频率就是1赫兹。如果钟摆每秒摆动5次,那么它的频率就是5赫兹。
二、频率的计算公式
频率的计算公式相对简单,可以用下面的公式表示:
f = N / T
其中:
f代表频率,单位为赫兹(Hz)
N代表在一定时间T内发生的事件次数
T代表测量频率的时间段,单位为秒(s)
举个例子,如果我们想计算一分钟内心跳的次数,可以这样操作:
1. 首先,记录下一段时间内(比如60秒)的心跳次数N。
2. 然后,将N除以T(60秒)。
3. 计算出来的结果就是心率的频率,单位是次/分钟(也可以用赫兹表示,不过这种情况下一般还是保留次/分钟这个单位,以便更符合常识)。
然而,通常情况下,心率会直接以每分钟跳动次数(BPM,即Beats Per Minute)来表示,不需要转换成赫兹。但是原理是相同的,都是用总数除以时间得到频率。
三、频率测量的应用
频率计算公式在各个领域都有广泛的应用,以下是几个具体的例子:
1. 音乐与声学:在音乐中,频率决定了音高。一个C4音符(中音C)的频率大约是261.63赫兹。通过使用乐器或者电子调音器,可以精确测量音符的频率,确保乐器的音调准确。
2. 物理学与工程学:在物理学和工程学中,频率被用于描述振动、波动等现象。比如,机械波、电磁波等都有频率的概念。频率的高低直接影响到波的性质和应用,如声波的频率决定了人耳是否能听到(人类能听到的声波频率范围是20赫兹到20千赫兹)。
3. 电子学与通信:在无线通信中,频率是一个核心参数。不同频段的电磁波用于不同的通信服务,如AM广播、FM广播、移动通信、卫星通信等。使用频率计算器可以确定一个信号占用的是哪个频段,以及是否有足够的带宽用于数据传输。
4. 生物医学:在生物医学领域,频率也扮演着重要角色。比如心电图(ECG)可以测量心脏跳动的频率,用于诊断心脏疾病。脑电图(EEG)可以测量大脑的电活动频率,用于研究脑功能和诊断神经系统疾病。
四、如何测量频率
要测量频率,需要两个关键的信息:一是事件的总次数N,二是测量这些事件所用的时间T。测量频率的方法因应用领域不同而有所差异,但基本原理是相似的。
1. 手动计数:对于简单的事件,如秒表测量跑步者的步频,可以通过手动计数的方法。记录下在一段时间内(比如30秒)的步数,然后乘以2得到每分钟的步频。
2. 电子设备:现代科技提供了更精确、便捷的测量频率的方法。电子频率计(也称为计数器)可以直接读取信号的频率,误差非常小。此外,很多数字万用表(DMM)也具备频率测量功能。
3. 软件分析:在计算机和数字化仪器中,可以使用软件对采集到的数据进行频率分析。比如,使用音频分析软件可以测量声音信号的频率;使用数据处理软件可以对时间序列数据进行频谱分析,找出信号的频率成分。
五、频率的误差与修正
任何测量都会有误差,频率测量也不例外。误差的来源可能是设备本身的精度限制,也可能是环境因素导致的干扰。
1. 设备精度:使用高精度的测量设备可以减小误差。例如,高级频率计具有非常小的误差范围,可以满足科研和工程中对高精度频率测量的需求。
2. 环境因素:环境中的电磁干扰、温度变化等都会影响频率测量的准确性。在进行精密测量时,需要尽量排除这些干扰因素,确保测量结果的可靠性。
3. 误差修正:在某些情况下,可以通过校准和修正的方法来减小误差。比如,使用校准频率源对测量设备进行校准,根据校准结果对测量结果进行修正。
六、总结
频率作为描述事件发生速率的重要参数,在我们的日常生活中无处不在。从音乐中的音调,到无线电波的传播,再到生物医学领域的信号处理,频率计算都发挥着关键作用。掌握频率计算公式和测量方法,可以帮助我们更好地理解和应用频率这个重要的物理量。
通过上述内容,相信你已经对频率计算公式有了较为深入的了解。无论是在理论学习还是在实际应用中,都能更自信地面对与频率相关的问题。记住,频率是事件在单位时间内发生的次数,这个简单的公式f = N / T,为我们揭示了一个丰富多彩的物理世界。
- 上一篇: 如何登录苹果官方网站?
- 下一篇: 如何找到手机百度APP的回收站位置
-
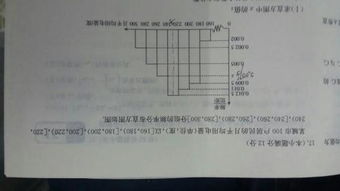 如何计算频率分布直方图的中位数?公式及应用详解新闻资讯10-27
如何计算频率分布直方图的中位数?公式及应用详解新闻资讯10-27 -
 揭秘:概率计算公式全解析新闻资讯10-25
揭秘:概率计算公式全解析新闻资讯10-25 -
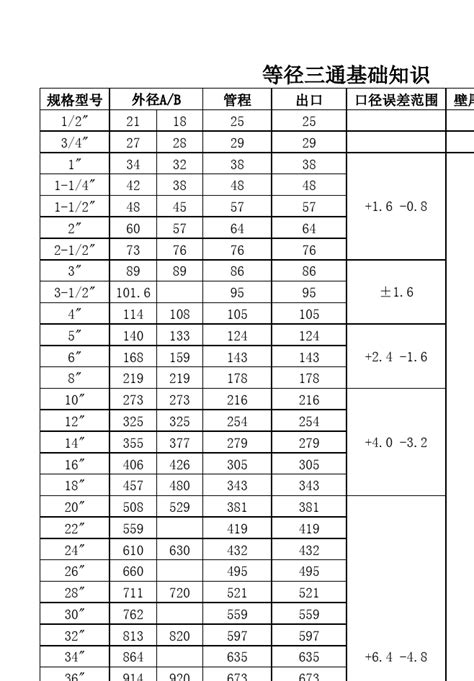 揭秘:重量计算公式全解析新闻资讯11-13
揭秘:重量计算公式全解析新闻资讯11-13 -
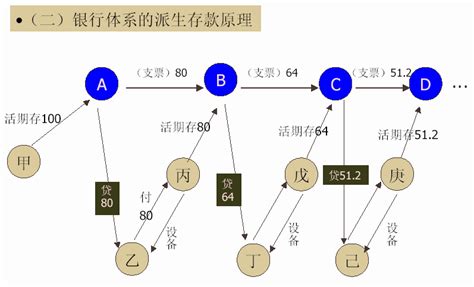 揭秘:货币乘数的计算公式全解析新闻资讯11-14
揭秘:货币乘数的计算公式全解析新闻资讯11-14 -
 揭秘:频率公式的定义与应用,你不可不知的实用知识!新闻资讯11-01
揭秘:频率公式的定义与应用,你不可不知的实用知识!新闻资讯11-01 -
 2023年退休金全新计算公式大揭秘新闻资讯11-12
2023年退休金全新计算公式大揭秘新闻资讯11-12