揭秘BCD码:全面了解二进制编码的十进制数
二进制编码的十进制数,简称BCD码(Binary-Coded Decimal),是一种将十进制数的每一位数字分别用二进制编码表示的方法。在计算机科学和数字电子学中,BCD码扮演着重要角色,特别是在需要直接处理十进制数的场合。这种编码方式不仅使人类阅读和机器处理十进制数变得方便,还在各种应用领域中,如计算器、数字仪表、金融计算系统等,展现出独特的优势。

BCD码的基本概念是将十进制数的每一位(0-9)转换成一个等价的四位二进制数。这种转换遵循的是一种固定对应关系:0对应0000,1对应0001,2对应0010,以此类推,直到9对应1001。这样,一个十进制数,比如123,就可以被编码为0001 0010 0011,其中每一位十进制数都被独立地转换成了相应的四位二进制数。
BCD码的优势之一在于它简化了人类与计算机之间的交互。由于十进制数是人们在日常生活中最熟悉的数制,因此使用BCD码能够使得计算机的输出结果更加直观易懂。例如,在计算器的显示屏上,使用BCD码编码的数字可以直接以十进制形式显示出来,而无需进行额外的转换。
除了直观性之外,BCD码还在某些特定的计算任务中提供了便利。在某些应用场景下,需要对十进制数进行精确计算,而二进制或十六进制数在这些任务中可能不够直观或难以处理。使用BCD码可以使得这些计算变得更加直接和高效。例如,在会计和金融领域,经常需要处理精确的货币计算,使用BCD码可以确保这些计算以十进制形式进行,从而避免了因舍入误差而导致的精度问题。
此外,BCD码在数字电路中也有着广泛的应用。在数字电子系统中,使用BCD码编码的十进制数可以方便地通过逻辑门电路进行算术运算和逻辑操作。由于BCD码每一位都是四位二进制数,因此可以很方便地利用现有的二进制电路来实现复杂的十进制运算。例如,加法器、减法器和乘法器等基本运算电路都可以使用BCD码来实现十进制数的运算。
当然,BCD码也有一些局限性。首先,由于每一位十进制数都需要用四位二进制数来表示,因此BCD码在存储和传输数据时效率较低。相比之下,二进制或十六进制数能够用更少的位数来表示相同的信息量。其次,BCD码的运算规则相对复杂,特别是在进行多位数运算时,需要考虑进位和借位等问题。这些复杂性增加了BCD码运算电路的设计和实现的难度。
尽管存在这些局限性,但BCD码在某些特定应用场景下仍然具有不可替代的优势。随着计算机技术的不断发展,BCD码的应用也在不断扩展和创新。例如,在嵌入式系统中,BCD码被广泛应用于各种数字仪表和显示设备中。这些设备通常需要以十进制形式显示测量结果或状态信息,而BCD码能够直接满足这一需求。
此外,BCD码还在一些高级应用中发挥着重要作用。例如,在数据通信领域,BCD码可以用于编码传输的十进制数据,以确保数据的准确性和可靠性。在图像处理领域,BCD码可以用于表示灰度级或颜色值等十进制信息,从而实现对图像的精确处理和分析。
值得注意的是,BCD码并不是唯一的十进制编码方式。除了BCD码之外,还有多种其他的十进制编码方法,如二进制加权码(Binary-Weighted Code)、格雷码(Gray Code)等。这些方法在不同的应用场景下具有各自的优势和局限性。因此,在选择十进制编码方式时,需要根据具体的应用需求进行权衡和选择。
总的来说,BCD码作为一种将十进制数转换为二进制编码的方法,在计算机科学和数字电子学中发挥着重要作用。它简化了人类与计算机之间的交互,提高了十进制数处理的直观性和效率。同时,BCD码还在各种应用领域中展现出独特的优势,如计算器、数字仪表、金融计算系统等。虽然BCD码存在一些局限性,但随着计算机技术的不断发展,它在特定应用场景下的优势仍然不可替代。
在实际应用中,BCD码的实现方式可以多种多样。例如,在硬件实现中,可以使用专门的BCD码运算电路来完成十进制数的算术运算和逻辑操作。在软件实现中,可以使用编程语言中的BCD码库函数或自定义函数来处理BCD码编码的十进制数。此外,还可以将BCD码与其他数制相结合,以实现更加灵活和高效的数据处理方式。
总之,BCD码作为一种重要的十进制编码方式,在计算机科学和数字电子学中发挥着重要作用。它以其独特的优势在各种应用领域中得到了广泛应用和发展。随着计算机技术的不断进步和创新,BCD码的应用前景将更加广阔和美好。
- 上一篇: 一键学会下载老来网应用
- 下一篇: 装潢与装璜有何区别?
-
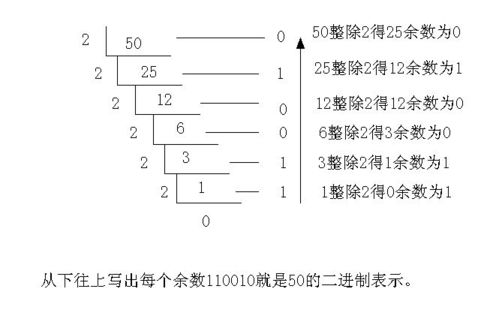 怎样把16进制数转换成10进制数?新闻资讯10-28
怎样把16进制数转换成10进制数?新闻资讯10-28 -
 问答揭秘:怎样迅速把十进制101转为八进制数?新闻资讯11-06
问答揭秘:怎样迅速把十进制101转为八进制数?新闻资讯11-06 -
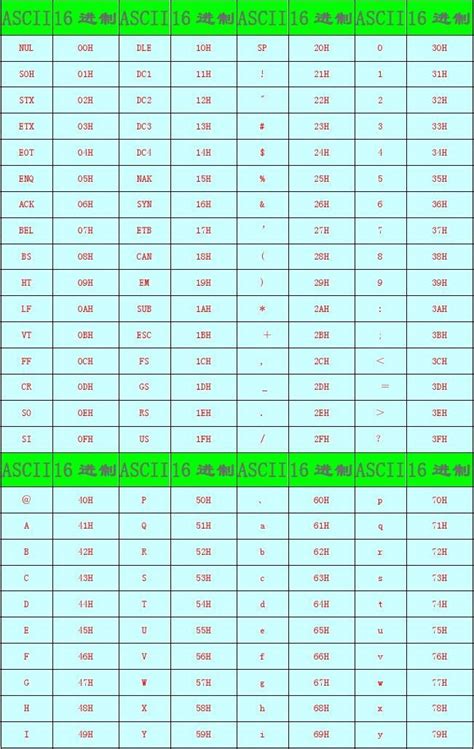 十六进制转换方法详解新闻资讯11-22
十六进制转换方法详解新闻资讯11-22 -
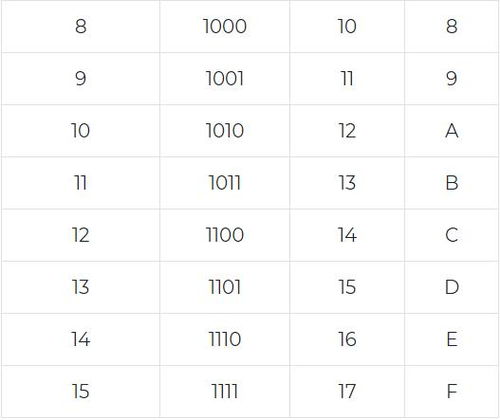 二进制与十六进制转换指南:轻松掌握转换技巧新闻资讯11-24
二进制与十六进制转换指南:轻松掌握转换技巧新闻资讯11-24 -
 如何将十进制数转换为八进制数?新闻资讯11-24
如何将十进制数转换为八进制数?新闻资讯11-24 -
 十进制轻松转换为八进制的方法新闻资讯11-06
十进制轻松转换为八进制的方法新闻资讯11-06








