十进制轻松转换为八进制的方法
十进制转换成八进制的方法

十进制数转换成八进制数,对于很多初学者来说可能是一个陌生的概念。但实际上,只要掌握了基本的转换规则,这个过程就会变得非常简单。本文将详细介绍如何将十进制数转换为八进制数,包括基础概念、具体步骤以及注意事项,帮助读者快速掌握这一技能。
首先,我们需要了解十进制、八进制的基本概念。十进制是我们日常生活中最常用的数制,它基于10个不同的数字符号(0、1、2、3、4、5、6、7、8、9)进行计数。而八进制则是一种基于8个不同数字符号(0、1、2、3、4、5、6、7)的数制。在计算机科学中,八进制常用于表示文件权限等场景。
十进制转换成八进制的核心思想是通过反复除以基数8,并记录每次的余数,直到商为0为止。然后将这些余数从最后一位开始依次排列,即可得到八进制数。下面,我们详细讲解转换步骤:
1. 确定要转换的十进制数:
假设我们要将十进制数123转换成八进制数。
2. 进行除法运算:
将十进制数除以8,并记录余数。然后将商继续除以8,直到商为0为止。每次除法的余数就是八进制数的一位。
123 ÷ 8 = 15 余 3
15 ÷ 8 = 1 余 7
1 ÷ 8 = 0 余 1
3. 记录余数并排列:
将每次除法的余数从最后一位开始依次排列,即得到八进制数。根据上面的计算过程,我们得到的余数是3、7、1。因此,十进制数123的八进制表示是173。
4. 验证转换结果(可选):
为了确认转换结果是否正确,我们可以将得到的八进制数转换回十进制数进行验证。八进制数转换成十进制数的方法是,将每一位上的数字乘以8的相应次方(从右往左,次方递增),然后将这些乘积相加。
173(八进制)= 1 × 8^2 + 7 × 8^1 + 3 × 8^0
= 64 + 56 + 3
= 123(十进制)
由于转换回十进制后的结果与原数相同,因此可以确认我们的转换是正确的。
接下来,我们通过一个更复杂的例子来进一步说明转换过程。假设我们要将十进制数255转换成八进制数。
1. 确定要转换的十进制数:
十进制数255。
2. 进行除法运算:
255 ÷ 8 = 31 余 7
31 ÷ 8 = 3 余 7
3 ÷ 8 = 0 余 3
3. 记录余数并排列:
余数依次是7、7、3。因此,十进制数255的八进制表示是377。
4. 验证转换结果(可选):
377(八进制)= 3 × 8^2 + 7 × 8^1 + 7 × 8^0
= 192 + 56 + 7
= 255(十进制)
验证结果正确。
此外,还有一些特殊情况需要注意:
零的转换:十进制数0的八进制表示也是0。这是因为任何数制中的0都是相同的。
小数的转换:对于包含小数部分的十进制数,我们可以分别转换其整数部分和小数部分。整数部分按照上述方法进行转换,小数部分则是通过反复乘以基数8,并记录每次的整数部分,直到小数部分为0或达到所需的精度为止。然后将这些整数部分从第一位开始依次排列(注意小数点的位置)。
例如,要将十进制小数0.625转换成八进制小数,我们可以这样做:
0.625 × 8 = 5(整数部分),0.000(小数部分,舍去)
因此,十进制小数0.625的八进制表示是0.5。
负数的转换:对于负数,我们可以先将其绝对值转换成八进制数,然后在前面加上负号。
通过上述步骤和注意事项,我们可以轻松地将任何十进制数转换成八进制数。无论是整数还是小数,无论是正数还是负数,都可以按照相应的方法进行转换。
最后,需要强调的是,十进制与八进制之间的转换是计算机科学中的基础知识之一。掌握这一技能不仅有助于我们更好地理解计算机内部
- 上一篇: 如何查阅卡方分布分位数表
- 下一篇: 酷狗直播开启直播教程:轻松上手直播步骤
-
 如何将十进制数转换为八进制数?新闻资讯11-24
如何将十进制数转换为八进制数?新闻资讯11-24 -
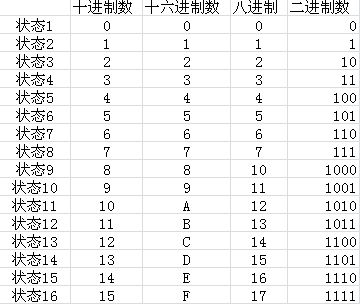 轻松掌握:二进制与十六进制数的相互转换方法新闻资讯11-07
轻松掌握:二进制与十六进制数的相互转换方法新闻资讯11-07 -
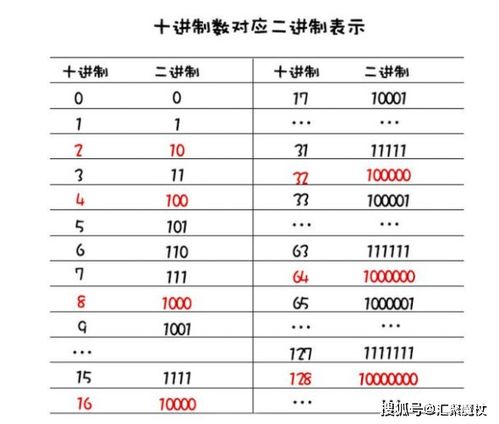 十六进制转换为十进制的方法新闻资讯11-12
十六进制转换为十进制的方法新闻资讯11-12 -
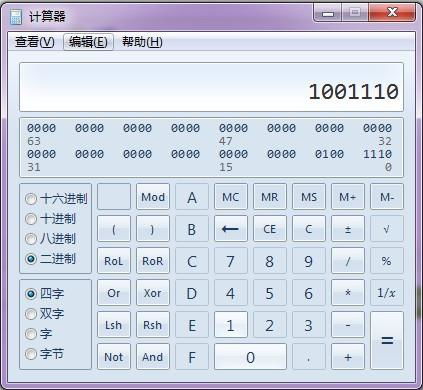 如何将十六进制快速转换为十进制(电脑计算器方法)新闻资讯11-11
如何将十六进制快速转换为十进制(电脑计算器方法)新闻资讯11-11 -
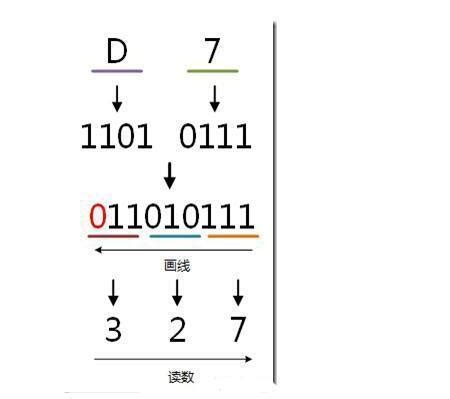 二进制与十六进制相互转换方法新闻资讯11-07
二进制与十六进制相互转换方法新闻资讯11-07 -
 轻松掌握:二进制与十六进制的转换方法新闻资讯11-24
轻松掌握:二进制与十六进制的转换方法新闻资讯11-24








