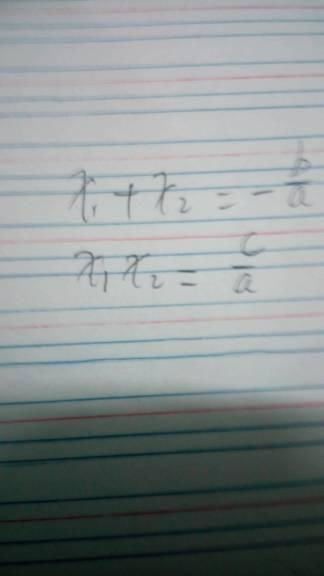八大根与系数关系公式详解
在数学的浩瀚宇宙中,一元二次方程占据着举足轻重的地位。它不仅连接了代数与几何的桥梁,更是揭示了数与形之间深刻的内在联系。而在这片领域中,根与系数的关系无疑是璀璨星辰中的一颗,它以其简洁而深刻的形式——韦达定理,引领我们探索方程解的奥秘。本文将详细介绍根与系数关系的八个重要公式,旨在帮助读者更全面、深入地理解这一核心概念。

根与系数关系的基石:韦达定理
首先,让我们回顾一下韦达定理的基本内容。对于一元二次方程ax²+bx+c=0(a≠0),若x1和x2是它的两个根,那么这两个根与方程系数之间存在如下关系:
x1+x2=-b/a
x1·x2=c/a
这两个公式构成了根与系数关系的基石,也是我们探索更多相关公式的基础。
公式一:根的平方和
在韦达定理的基础上,我们可以推导出根的平方和公式。利用平方差公式和韦达定理,我们有:
x1²+x2²=(x1+x2)²-2x1x2=(-b/a)²-2(c/a)=(b²-2ac)/a²
这个公式在求解与根的平方相关的代数式时非常有用。
公式二:根的乘积的平方和
类似地,我们还可以推导出根的乘积的平方和公式。这个公式在求解涉及根的乘积平方的代数式时同样重要:
x1²x2+x1x2²=x1x2(x1+x2)=c/a*(-b/a)=-bc/a²
公式三:根的倒数和
在求解根的倒数相关的代数式时,我们可以利用韦达定理推导出根的倒数和公式:
1/x1+1/x2=(x1+x2)/(x1x2)=-b/c
公式四:根的比值和
有时候,我们需要求解根的比值和。通过韦达定理和代数变换,我们可以得到:
x2/x1+x1/x2=(x2²+x1²)/(x1x2)=((x1+x2)²-2x1x2)/(x1x2)=((b/a)²-2(c/a))/(c/a)=(b²-2ac)/(ac)
公式五:根的线性组合
在求解根的线性组合相关的代数式时,我们可以利用韦达定理和代数恒等式进行推导。例如,对于(x1+p)(x2+p)这样的表达式,我们有:
(x1+p)(x2+p)=x1x2+p(x1+x2)+p²=c/a+p(-b/a)+p²=(ap²+cp-bp)/a
公式六:根的差的平方
在求解根的差的平方时,我们可以利用平方差公式和韦达定理进行推导:
(x1-x2)²=(x1+x2)²-4x1x2=(-b/a)²-4(c/a)=(b²-4ac)/a²
这个公式在求解与根的差相关的代数式时非常有用,尤其是在判断方程根的性质时。
公式七:根的对称代数式
韦达定理及其推广还可以用于求解根的对称代数式的值。例如,对于x1³+x2³这样的表达式,我们可以利用立方和公式和韦达定理进行推导:
x1³+x2³=(x1+x2)(x1²-x1x2+x2²)=(x1+x2)((x1+x2)²-3x1x2)=(-b/a)((-b/a)²-3(c/a))=-b³/a³+3bc/a²
类似地,我们还可以推导出其他对称代数式的值。
公式八:构造一元二次方程
韦达定理的逆定理指出,如果两个数的和与积分别等于一元二次方程的两个系数(注意顺序和符号),则这两个数就是该方程的两个根。这个逆定理为我们提供了一种构造一元二次方程的方法。例如,如果我们知道两个数的和为s,积为p,那么我们可以构造出方程x²-sx+p=0,这两个数就是该方程的两个根。
应用实例
为了更好地理解这些公式,让我们来看一些应用实例。
实例一:已知x1和x2是方程x²-4x+3=0的两个根,求1/x1+1/x2的值。
根据韦达
- 上一篇: 微信查找附近的人使用指南
- 下一篇: 微信怎么进行转账?
-
 揭秘!韦达定理公式全解析:你不得不知的数学奥秘新闻资讯10-20
揭秘!韦达定理公式全解析:你不得不知的数学奥秘新闻资讯10-20 -
 相关系数r的具体计算公式是什么新闻资讯11-23
相关系数r的具体计算公式是什么新闻资讯11-23 -
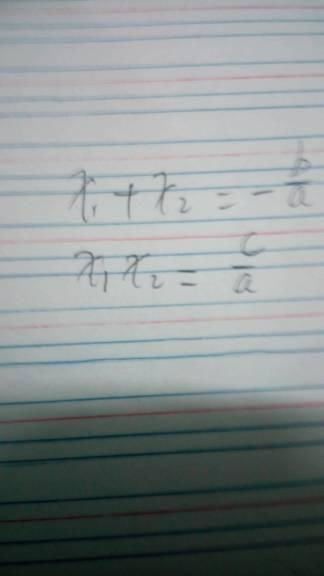 揭秘数学奇迹:韦达定理公式,解开多项式根之迷的钥匙!新闻资讯10-19
揭秘数学奇迹:韦达定理公式,解开多项式根之迷的钥匙!新闻资讯10-19 -
 如何准确计算快递体积费用?新闻资讯06-04
如何准确计算快递体积费用?新闻资讯06-04 -
 椭圆的标准公式详解新闻资讯11-07
椭圆的标准公式详解新闻资讯11-07 -
 揭秘!如何在Excel中轻松计算线性相关系数新闻资讯03-23
揭秘!如何在Excel中轻松计算线性相关系数新闻资讯03-23