揭秘三角形相似的奥秘:全面解析判定方法
在探讨几何学中,三角形相似的判定方法占据了至关重要的地位。这些判定方法不仅为我们提供了一种解决与三角形相关问题的新思路,更是几何学理论与实践紧密结合的体现。接下来,我们将深入讨论几种主要的三角形相似的判定方法,通过详细的阐述和实例分析,帮助读者更好地理解和掌握这些技巧。

首先,最为基础且直观的三角形相似判定方法是角角相似(AA相似)。该定理指出,如果两个三角形中有两对对应的角分别相等,则这两个三角形必定相似。角角相似的理论依据在于,角度的相等性决定了三角形的形状,只要两个三角形的角度对应相等,其边长比例也会相应保持一致。以数学表达式表述,设两个三角形分别为△ABC和△DEF,若∠A=∠D,∠B=∠E,则△ABC∽△DEF。角角相似不仅简洁明了,而且在实际应用中十分便捷,尤其是当我们无法通过直接测量边长来确定三角形是否相似时,只需测量并比较相应的角度即可。

紧接着,我们来看看角边角相似(ASA相似)。这个判定方法告诉我们,如果两个三角形中有一对角分别相等,并且这一对对角所夹的边也成比例,那么这两个三角形相似。用数学语言表述,即若∠A=∠D,∠B=∠E,且AB/DE=BC/EF,则△ABC∽△DEF。与角角相似相比,角边角相似引入了边长比例的元素,因此在处理一些更复杂的几何问题时显得更为强大。值得注意的是,这里的边长比例关系并不是由我们事先知道或假设的,而是通过测量得到的。也就是说,只有当我们确认了角度相等性和边长比例之后,才能应用角边角相似定理。

除了角角相似和角边角相似之外,还有一种较为常见的三角形相似判定方法是边角边相似(SAS相似)。该方法表明,如果两个三角形中有一对对应边成比例,并且这对边所夹的角也相等,则这两个三角形相似。在数学表达式中,如果AB/DE=AC/DF,且∠A=∠D,则△ABC∽△DEF。边角边相似与角边角相似有一定的相似性,但在实际使用中,边角边相似更注重边长比例和角度相等的双重条件。这使得它在处理一些特定的几何问题时,具有独特的优势。

另外,我们不能忽视的一种三角形相似判定方法是HL相似(Hypotenuse-Leg相似)。这是一种专门用于直角三角形相似性的判定方法。它指出,如果两个直角三角形的一条直角边和斜边分别成比例,则这两个直角三角形相似。即对于直角三角形△ABC和△DEF,若AC=直角边,BC=斜边,DF=直角边,EF=斜边,且AC/DF=BC/EF,则△ABC∽△DEF。HL相似是直角三角形相似判定的一种特殊形式,它不仅简化了直角三角形的相似性判断过程,还为后续的相关计算和证明提供了便利。
值得一提的是,以上四种三角形相似的判定方法并非孤立存在,它们之间有着密切的联系和相互支持。例如,在解决一些复杂的几何问题时,我们可能需要同时利用角角相似和边角边相似等多种判定方法,以便从多个角度进行论证和推理。此外,这些判定方法在实际应用中往往需要根据问题的具体情况进行选择和调整,以达到最佳效果。
接下来,让我们通过一些具体的例子来进一步巩固和深化对三角形相似判定方法的理解。例如,已知两个三角形△ABC和△DEF,其中∠A=∠D,∠B=∠E,我们需要证明这两个三角形相似。此时,我们可以直接应用角角相似定理,得出△ABC∽△DEF。再例如,若已知两个三角形△GHI和△JKL,其中GI/JL=HI/KL,且∠G=∠J,我们则可以利用边角边相似定理来证明这两个三角形相似。
除了基本的判定方法外,我们还可以通过一些其他的数学工具和技巧来辅助我们判断三角形的相似性。例如,通过利用勾股定理来计算直角三角形的边长比例,或者通过构建辅助线来转化非直角三角形为直角三角形等。这些技巧和方法不仅丰富了我们判断三角形相似性的手段,也为我们解决更复杂的几何问题提供了有力支持。
当然,在应用三角形相似的判定方法时,我们还需要注意一些细节和陷阱。例如,对于角角相似和角边角相似来说,角度的相等性必须是对应角之间的相等性,而不是任意角之间的相等性。同时,边长比例的计算也需要精确无误,以避免出现错误的结论。此外,对于HL相似来说,我们必须确保所讨论的两个三角形是直角三角形,否则该判定方法将不再适用。
总的来说,三角形相似的判定方法是几何学中的重要组成部分。通过学习和掌握这些判定方法,我们不仅可以更好地理解三角形的性质和关系,还可以运用这些方法来解决与三角形相关的各种问题。因此,建议读者在学习过程中注重理论与实践的结合,通过不断的练习和实践来加深对这些判定方法的理解和掌握。
在几何学的学习和研究中,三角形相似的判定方法是一个重要的工具。它不仅可以简化问题的解决过程,还可以提高我们的几何直觉和解题能力。因此,我们应该认真学习和
- 上一篇: 掌握"remaining"与"remained"的精准区别
- 下一篇: 正本清源的含义是什么
-
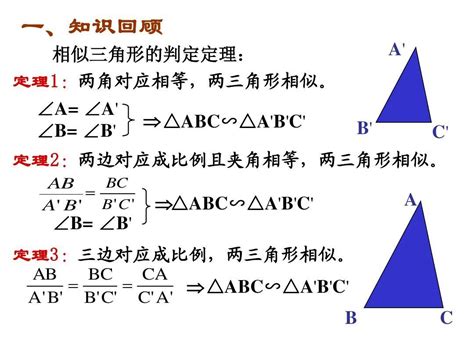 怎样确定两个三角形是否相似?新闻资讯11-03
怎样确定两个三角形是否相似?新闻资讯11-03 -
 全等三角形的判定方法新闻资讯11-05
全等三角形的判定方法新闻资讯11-05 -
 全等三角形的六种判定条件是什么?新闻资讯12-05
全等三角形的六种判定条件是什么?新闻资讯12-05 -
 揭秘正交矩阵:四大精妙判定法,轻松解锁矩阵世界奥秘新闻资讯10-30
揭秘正交矩阵:四大精妙判定法,轻松解锁矩阵世界奥秘新闻资讯10-30 -
 掌握这几种技巧,轻松判断全等三角形!新闻资讯11-24
掌握这几种技巧,轻松判断全等三角形!新闻资讯11-24 -
 如何证明全等三角形的方法有哪些?新闻资讯11-05
如何证明全等三角形的方法有哪些?新闻资讯11-05












