如何计算梯形面积?
梯形面积,原来这么简单!

在日常生活中,我们经常会遇到各种形状和大小的图形,它们有的简单有的复杂,但每一种图形都有其独特的魅力和计算方法。今天,我们就来聊聊一种既常见又实用的几何图形——梯形,特别是关于如何计算它的面积。
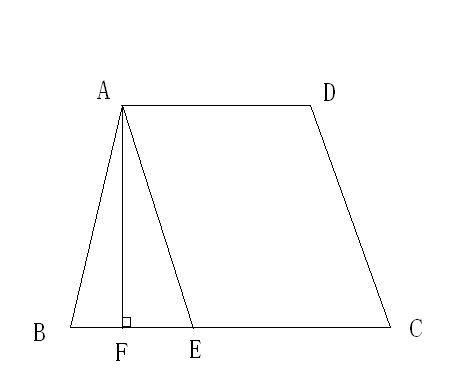
梯形,听起来可能有点陌生,但其实它就在我们身边。比如,你手中的梯形笔筒、墙上挂着的梯形装饰画,还有校园里那些梯形花坛,都是梯形在生活中的实际应用。那么,当我们需要知道这些梯形的面积时,应该怎么办呢?别担心,接下来我们就来揭开梯形面积的神秘面纱。

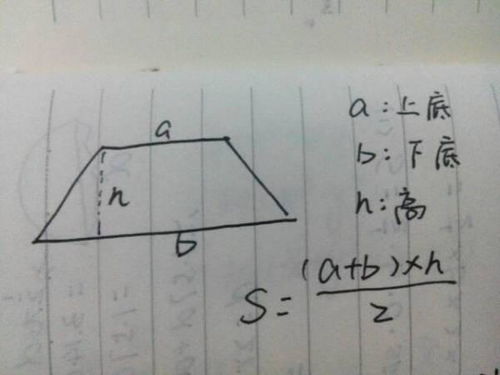
首先,我们要明确梯形的定义。梯形是指一组对边平行且不相等的四边形。这组平行的对边,我们称之为梯形的上底和下底,其中较短的那条边通常被称为上底,较长的那条边则被称为下底。而梯形另外两条不平行的边,我们称之为梯形的腰。

了解了梯形的定义后,我们就可以开始探讨如何计算梯形的面积了。在几何学中,梯形面积的计算有一个非常简洁且实用的公式,那就是:
梯形面积 = (上底 + 下底) × 高 ÷ 2
这个公式看起来很简单,但其中却蕴含着深刻的几何原理。为了更好地理解这个公式,我们可以从梯形的构造和性质入手。
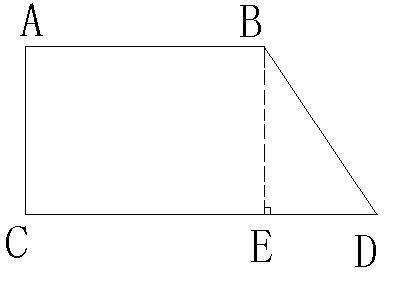
想象一下,如果我们有一个梯形,我们可以尝试将它分解成一个矩形和两个三角形。具体做法是:过梯形的一个顶点(不是上底和下底的顶点),作一条垂直于下底的直线,这条直线与下底相交于一点,同时也将梯形分割成了一个矩形和两个三角形。接着,我们可以将这两个三角形进行拼接,得到一个大的三角形,这个三角形的底就是梯形的上底和下底之和,而高就是梯形的高。
现在,我们来看看这个大的三角形的面积应该怎么计算。根据三角形面积的计算公式:
三角形面积 = 底 × 高 ÷ 2
我们可以得到这个大三角形的面积为:
(上底 + 下底) × 高 ÷ 2
而由于这个大的三角形是由梯形分解出来的,所以它的面积就等于梯形的面积。因此,我们就得到了梯形面积的计算公式:
梯形面积 = (上底 + 下底) × 高 ÷ 2
这个公式不仅简洁明了,而且非常实用。只要我们知道梯形的上底、下底和高,就可以轻松地计算出梯形的面积了。
当然,在实际应用中,我们可能会遇到一些特殊情况。比如,有些梯形的上底和下底可能并不是水平的,而是倾斜的。这时候,我们只需要将梯形旋转到一个合适的角度,使得上底和下底变得水平,然后就可以使用上述的公式进行计算了。
另外,还有一些梯形的形状可能比较复杂,比如它们的腰可能不是直线而是曲线。对于这种情况,我们可以尝试将梯形分割成更小的、形状更简单的图形(如矩形、三角形、梯形等),然后分别计算这些图形的面积,最后将它们加起来就得到了梯形的总面积。这种方法虽然比较繁琐,但也是一种有效的解决方案。
除了上述的计算方法外,我们还可以利用一些现代的科技手段来辅助我们计算梯形的面积。比如,我们可以使用各种几何绘图软件或计算器来绘制梯形并计算其面积。这些工具通常都提供了非常精确和高效的计算方法,可以大大简化我们的计算过程。
不过,需要注意的是,虽然这些工具可以帮助我们快速得到结果,但我们应该始终理解并掌握梯形面积的基本计算方法。因为只有这样,我们才能在遇到各种复杂情况时灵活运用所学知识,解决实际问题。
此外,梯形面积的计算还有一些有趣的应用。比如,在建筑设计中,设计师常常需要计算各种形状和大小的梯形的面积,以确保建筑物的结构稳定性和美观性。在农业生产中,农民也需要计算梯形田地的面积,以便合理安排种植计划和施肥量。在地理学和测绘领域,梯形面积的计算也扮演着重要的角色,它可以帮助我们更准确地了解地球表面的形状和大小。
总之,梯形面积的计算虽然看似简单,但其中却蕴含着丰富的几何原理和实际应用价值。通过学习和掌握梯形面积的计算方法,我们不仅可以更好地理解几何学的奥秘,还可以将这些知识应用到实际生活中去,解决各种实际问题。
所以,下次当你再看到那些梯形形状的物体时,不妨试着用你所学的知识去计算一下它们的面积吧!你会发现,原来梯形面积的计算也可以变得如此有趣和实用。而且,随着你对几何学的不断深入了解,你还会发现更多关于梯形和其他几何图形的奇妙之处。让我们一起在几何学的世界里畅游吧!
- 上一篇: 揭秘梯形面积计算的奥秘
- 下一篇: 掌握千牛卖家工作台的高效操作方法
-
 梯形体积该如何计算?新闻资讯11-12
梯形体积该如何计算?新闻资讯11-12 -
 揭秘梯形面积计算的奥秘新闻资讯10-30
揭秘梯形面积计算的奥秘新闻资讯10-30 -
 如何计算梯形的面积?新闻资讯10-24
如何计算梯形的面积?新闻资讯10-24 -
 梯形面积计算公式新闻资讯12-02
梯形面积计算公式新闻资讯12-02 -
 揭秘梯形面积计算的奥秘公式新闻资讯10-30
揭秘梯形面积计算的奥秘公式新闻资讯10-30 -
 揭秘梯形面积计算的奥秘:一键掌握高效公式新闻资讯12-22
揭秘梯形面积计算的奥秘:一键掌握高效公式新闻资讯12-22