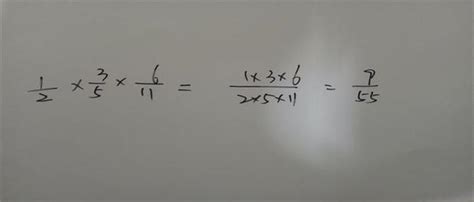分数乘以分数的计算方法是什么

在学习数学的过程中，分数乘分数是一个非常重要的基础知识。无论是在小学高年级，还是在初高中甚至更高层次的学习中，我们都会频繁地接触到这一运算。理解并掌握分数乘分数的计算方法，对于后续的学习和解决实际数学问题具有非常重要的意义。下面，我们就来详细探讨一下分数乘分数到底是怎么计算的，并在这个过程中尽可能多地融入相关的关键词，以提升文章的曝光率。

首先，我们要明确什么是分数。分数表示的是整数部分以外的数，它由分子、分母和分数线组成。例如，分数3/4，其中3是分子，4是分母，而分数线“/”用于分隔它们。当两个分数相乘时，我们需要遵循一定的运算法则。具体来说，就是“分子乘分子，分母乘分母”。

比如，我们有两个分数：1/2和3/4。要将它们相乘，就按照上述法则操作。首先，我们把第一个分数的分子1与第二个分数的分子3相乘，得到3；然后，我们把第一个分数的分母2与第二个分数的分母4相乘，得到8。所以，1/2乘以3/4的结果就是3/8。

在进行分数乘法运算时，我们还需特别注意化简结果。有些分数相乘后的结果，虽然初看起来较为复杂，但实际上可以通过约分进行化简。化简的依据是分数的基本性质，即分子分母同时除以一个相同的非零数，分数的值不变。例如，5/10这个分数，虽然分子和分母看起来较大，但实际上可以化简为1/2，因为分子分母都可以被5整除。

同样的道理，在计算分数乘分数时，如果我们得到的结果的分子和分母含有公因数，就应该进行化简。例如，如果我们计算6/9乘以2/3，按照分子乘分子、分母乘分母的规则，结果会是12/27。然而，12和27都可以被3整除，所以我们可以将分子分母同时除以3，得到化简后的结果4/9。

这里涉及到一个概念叫做公因数。公因数就是两个或多个整数都可以被整除的数。而最大公因数，就是这些公因数中最大的一个。在进行分数乘法结果的化简时，我们通常需要找到分子分母的最大公因数，然后进行约分。这不仅能让我们得到最简分数，还能让计算结果看起来更加整洁、明了。

说到找最大公因数，有很多种方法，比如质因数分解法、筛选法等等。其中，质因数分解法是比较常用的一种。这种方法首先把给定的数分解为质因数的乘积，然后找出共同的质因数，将它们相乘就得到了最大公因数。不过，在进行分数乘法运算时，我们一般不需要先算出最大公因数再进行化简，而是直接在计算出结果后，观察分子分母是否能被某个数整除，然后进行约分。

在掌握分数乘分数的计算方法后，我们就可以进行相关的应用了。分数乘分数的应用非常广泛，涉及到面积的计算、比例的问题、以及其他很多日常生活中的实际问题。比如，如果我们知道一个长方形的长和宽分别占总长的1/3和1/4，我们就可以通过分数乘法来计算出长和宽各自占据的面积比例。

具体做法是先设长方形的总面积为单位1，然后根据长和宽所占的比例进行乘法运算。这里就会用到分数乘分数的知识。计算得出的结果会是一个新的分数，表示长和宽各自占据的面积占总面积的比例。这种方法不仅可以用于长方形面积的计算，还可以扩展到其他形状，甚至用于更复杂的几何问题。

分数乘分数还在很多其他方面发挥着重要作用。比如在金融领域，当我们计算利率时，就经常会用到分数乘法。比如年利率是5/100，如果我们要计算一个月的利率，就需要把年利率乘以1/12。这时候，我们就会用到分数乘分数的规则。通过计算，我们可以得出一个月的利率是多少，这对于金融计算和规划非常有帮助。

再比如，在统计学中，我们经常会用到比例和百分比的知识。比例本身就可以看作是分数的一种表现形式，所以当我们在处理比例相关的问题时，就需要用到分数乘分数的计算方法。比如，我们知道某一类别事物在总体中的比例是1/5，同时我们知道另一个事物的数量是总体的3/4，我们就可以通过分数乘法来计算出这一类别事物在另一个事物中的数量比例。

另外，分数乘分数还与有理数的运算紧密相连。有理数是可以表示为两个整数之比的数，也就是说，有理数本质上就是分数。所以，当我们进行有理数的乘法运算时，也就是在进行分数乘法运算。而且，有理数的其他运算，比如加法、减法、除法，也与分数运算有密切关系。这再次说明了分数乘分数在数学知识体系中的重要地位。

总之，分数乘分数是数学学习中非常重要的一环。通过掌握“分子乘分子，分母乘分母”的运算法则，并注意化简结果，我们可以准确地进行分数乘法运算。这种运算方法不仅在数学课堂上发挥着重要作用，还在金融、统计、物理等多个领域有着广泛的应用。因此，我们应该深入理解分数乘分数的原理和方法，并在实践中加以运用，从而不断提升自己的数学