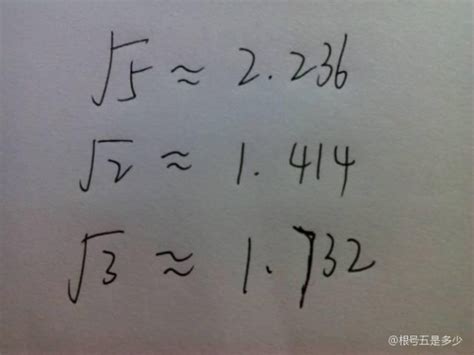根号5(√5)大约等于多少?
当我们探讨“√5约等于多少呢”这个问题时,实际上是在寻找一个无理数(即不能表示为两个整数的比的数)的近似值。根号5,在数学中表示为√5,是一个常见的无理数,它在几何、代数及物理学的多个领域都有广泛应用。虽然我们不能精确地用一个有限小数或分数来表示它,但我们可以利用多种方法来得到它的近似值。

直接计算与近似值
首先,我们可以直接通过计算器或数学软件来求√5的精确值,但通常情况下,为了简化问题或满足特定需求,我们会采用四舍五入等方法得到一个近似值。例如,使用计算器,我们可以得到√5约等于2.2360679775...。在大多数日常或科学计算中,我们可能只需要保留几位小数,因此,√5可以近似为2.24(保留两位小数)或2.236(保留三位小数)。
逼近方法
除了直接使用计算器外,我们还可以通过一些数学方法来逼近√5的值,这些方法不仅能帮助我们理解无理数的概念,还能在没有计算器的情况下进行估算。
1. 牛顿迭代法(Newton's method)
牛顿迭代法是一种在实数域和复数域上近似求解方程的方法。对于√5,我们可以将其转化为求解方程$x^2 - 5 = 0$的正根问题。选择一个初始近似值(比如2,因为$2^2 = 4$接近5),然后通过迭代公式不断逼近真实解。迭代公式为:
$$ x_{n+1} = \frac{1}{2} \left( x_n + \frac{5}{x_n} \right) $$
从$x_0 = 2$开始迭代几次,可以逐渐逼近√5的真实值。
2. 连续分数表示
√5也可以表示为无限连续分数的形式,这为我们提供了另一种逼近其值的方法。√5的连续分数表示为[2; 4, 4, 4, ...],这意味着:
$$ \sqrt{5} = 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \cdots}}} $$
通过这个表达式,我们可以截取连续分数的有限部分来得到√5的近似值。例如,只取前两项,就得到√5 ≈ 2 + 1/4 = 2.25,虽然这个近似值相对粗糙,但它展示了连续分数在逼近无理数方面的应用。
实际应用
了解√5的近似值不仅有助于我们进行数学计算,还能在多个领域找到其实际应用。例如:
几何学:在正方形对角线长度与边长关系的研究中,正方形对角线长度是其边长的√2倍,但当我们考虑一个边长为1、对角线长度为√5的五边形时(特别是正五边形),√5就直接关联到该五边形的几何特性上。
物理学:在某些物理模型中,√5可能作为某个关键参数的精确值或近似值出现,如共振频率的计算、波动方程的解等。
工程学:在工程设计中,特别是涉及比例、尺寸和优化的计算时,√5及其近似值可能会被用作参考标准或计算依据。
结论
综上所述,√5作为一个重要的无理数,在数学、物理、工程等多个领域都有广泛的应用。虽然我们不能精确地用一个有限小数或分数来表示它,但通过使用计算器、数学逼近方法(如牛顿迭代法、连续分数)等手段,我们可以得到其近似值。在实际应用中,这些近似值往往足够精确,能够满足我们的需求。因此,当我们被问及“√5约等于多少呢”时,可以6自信地回答:它约等于2.23(或其他根据需要保留的小数位数)。
- 上一篇: 根号5的精确值及计算方法
- 下一篇: 揭秘'same'的英文魔力:它的多重含义与日常生活中的神奇运用!
-
 探寻根号5(√5)的近似值是多少?新闻资讯10-28
探寻根号5(√5)的近似值是多少?新闻资讯10-28 -
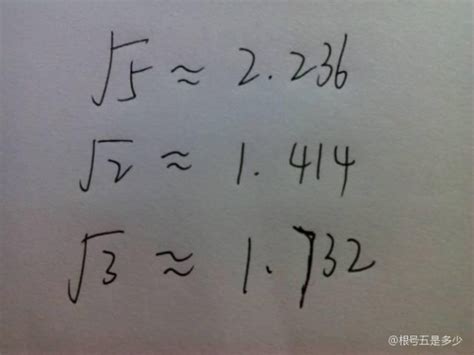 根号5的精确值及计算方法新闻资讯10-28
根号5的精确值及计算方法新闻资讯10-28 -
 5升水大约等于多少斤?新闻资讯12-04
5升水大约等于多少斤?新闻资讯12-04 -
 七寸照片的尺寸是多少?新闻资讯11-10
七寸照片的尺寸是多少?新闻资讯11-10 -
 揭秘!为何5升食用油并非等于10斤,重量与容量的奥秘新闻资讯10-25
揭秘!为何5升食用油并非等于10斤,重量与容量的奥秘新闻资讯10-25 -
 一升水等于多少斤?新闻资讯10-30
一升水等于多少斤?新闻资讯10-30