平移的定义是什么?它有哪些基本性质?
平移,作为几何学中一个基础而重要的概念,广泛存在于我们的日常生活与数学学习中。它描述了一种图形在平面内沿某一方向移动一定距离而不发生形状、大小变化的运动方式。这种看似简单的变换,实则蕴含了丰富的数学性质与应用价值,是理解更复杂几何变换和空间概念的基础。下面,我们将围绕“平移的定义与性质”这一主题,深入探讨其内涵。

平移的定义
平移,顾名思义,即“平行移动”的简称。在数学上,它指的是将一个图形(点、线段、多边形、圆等)沿着某一方向(通常是水平、垂直或两者之间的任意角度)移动一定的距离,而不改变图形的形状、大小以及图形内各元素之间的相对位置关系。这种变换只涉及位置的改变,不涉及旋转、缩放或反射等其他几何变换。
具体而言,若图形A经过平移后得到图形B,则图形A与图形B是完全重合的,只是位置不同。在平面直角坐标系中,平移可以通过加(或减)一个常数到图形上每个点的横坐标和(或)纵坐标上来实现。例如,一个点P(x, y)沿x轴正方向平移a个单位,沿y轴正方向平移b个单位后,新的位置为P'(x+a, y+b)。
平移的性质
平移作为一种基本的图形变换,具有一系列独特的性质,这些性质不仅帮助我们更好地理解和应用平移,也是解决相关数学问题的关键。
1. 形状与大小不变性:平移不会改变图形的形状和大小,即原图形与平移后的图形是全等的。这意味着图形中的所有线段长度、角度大小以及面积等度量性质在平移前后都保持不变。
2. 方向性与距离性:平移具有明确的方向和距离。方向可以是水平、垂直或任意给定的角度,距离则是图形上任意一点沿该方向移动的长度。这两个要素共同决定了平移的唯一性。
3. 相对位置关系不变:平移过程中,图形内各点之间的相对位置关系保持不变。例如,如果点A在点B的左侧,那么平移后,点A'(A的平移对应点)仍然在点B'(B的平移对应点)的左侧,且两者之间的相对距离也与原图中相同。
4. 平移的复合性:连续进行两次或多次平移,其结果等价于一次单独的平移。这一性质在数学上被称为平移的“可加性”,它极大地简化了平移变换的计算和描述。具体来说,若图形首先沿某一方向平移一定距离,再沿另一方向平移另一距离,则总的平移效果等同于直接沿一个合成方向(可能不是简单的水平或垂直)平移一个合成距离。
5. 与坐标系的关联:在平面直角坐标系中,平移可以通过坐标变换来精确描述和计算。这种关联不仅使平移具有了数值化的表达形式,也为解决平移相关的实际问题提供了有力的数学工具。
6. 平移的逆变换:每一个平移变换都有一个与之对应的逆变换,即沿相反方向移动相同的距离。这种逆变换使得图形能够回到其原始位置,体现了平移变换的可逆性。
平移的应用
平移不仅是一个抽象的数学概念,更广泛应用于现实生活与各个学科领域。在建筑设计中,平移常被用于模拟建筑元素在不同位置下的视觉效果;在计算机图形学中,平移是实现图形移动、动画效果的基本手段之一;在物理学中,平移运动是物体在不受外力作用或合外力为零时的一种理想运动状态;在地理学上,研究板块构造、地壳运动时,平移也是描述地壳块体相对运动的重要方式之一。
综上所述,平移作为几何学中的一个核心概念,其定义明确、性质丰富、应用广泛。通过对平移的深入学习,我们不仅能够掌握这一基本的图形变换方法,还能进一步拓展我们的数学视野,提升解决实际问题的能力。
- 上一篇: 股市新手必看!轻松几步教你完成股票开户流程
- 下一篇: 蒯姓的正确读音是什么?
-
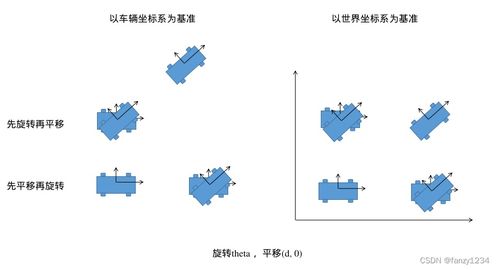 揭秘!平移与旋转:定义、差异与视觉盛宴的奥秘新闻资讯10-28
揭秘!平移与旋转:定义、差异与视觉盛宴的奥秘新闻资讯10-28 -
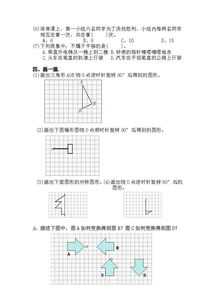 探索数学的奇妙之旅:揭秘平移的神奇定义(小学数学版)新闻资讯11-23
探索数学的奇妙之旅:揭秘平移的神奇定义(小学数学版)新闻资讯11-23 -
 单项式包含哪些内容?新闻资讯11-13
单项式包含哪些内容?新闻资讯11-13 -
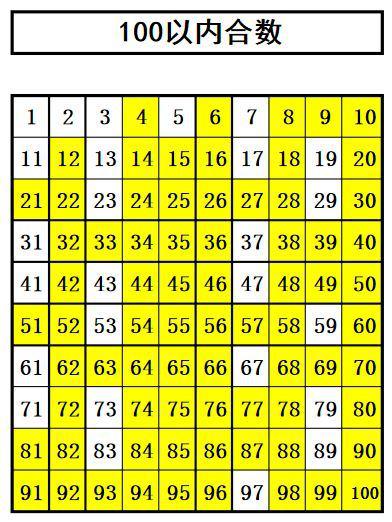 揭秘!你知道哪些数字是神秘的素数吗?新闻资讯10-23
揭秘!你知道哪些数字是神秘的素数吗?新闻资讯10-23 -
 邮箱地址的定义与说明新闻资讯11-14
邮箱地址的定义与说明新闻资讯11-14 -
 邮箱地址的定义与用途新闻资讯11-24
邮箱地址的定义与用途新闻资讯11-24












