质数表口诀是什么?
质数表的口诀详解

质数,又称素数,是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。在数论中,质数的应用非常广泛,它们不仅是数学研究的重要对象,还在密码学、计算机科学等领域发挥着重要作用。为了帮助记忆和识别质数,人们总结出了一些口诀,这些口诀不仅简洁明了,还具有一定的趣味性,使得学习和记忆质数变得更加轻松。

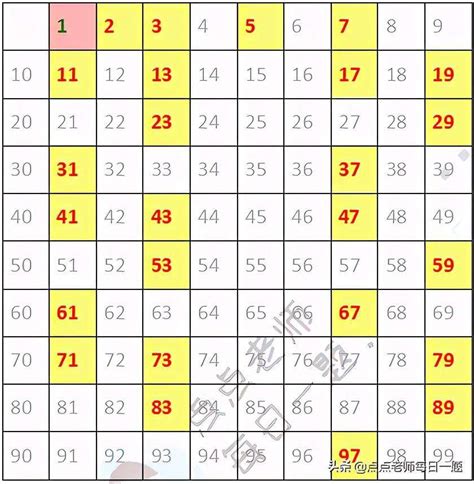
口诀一:“二、三、五、七、十一,十三、十七、十九。”

这是质数表中最初的几个质数,也是最常见的质数。这些质数在数轴上依次排列,彼此之间没有其他的质数插入。这个口诀简单明了,通过反复诵读,可以迅速记住这些基本的质数。
口诀二:“三十以前质数七,四位五,尾带一。”
这句口诀进一步扩展了质数的范围,涵盖了30以内的所有质数。其中,“三十以前质数七”指的是30以内的质数有7个,分别是2、3、5、7、11、13、17、19(虽然列出了8个数,但按照口诀的语境,“七”指的是数量而非具体数字,且此处可能为了凑韵而稍有出入,实际应为前10个自然数中去掉4个合数4、6、8、9后的7个质数)。而“四位五,尾带一”则是对这些质数特征的描述,其中“四位五”可以理解为将2、3、5、7这四个质数看作一组(尽管只有四个,但此处可能是为了凑数或方便记忆而如此表述),再加上后面的11、13、17、19这四个以1结尾的质数,就构成了30以内的所有质数。当然,这种解释略显牵强,但口诀本身旨在便于记忆,无需过于深究。
口诀三:“六一、六七、七十一,七三、七九、八十三。”
这句口诀涵盖了60到90之间的部分质数。通过这句口诀,我们可以迅速记住61、67、71、73、79、83这几个质数。这些质数在数轴上分布较为均匀,且相邻之间没有其他质数插入。
口诀四:“九七、加一得质百。”
这句口诀指的是97之后的下一个质数是101,也就是“质百”(即质数中的第一百个左右,此处为形象说法,并非确切指第一百个质数)。通过这句口诀,我们可以记住97和101这两个相邻的质数。
除了以上这些具体的口诀外,还有一些更通用的方法可以帮助我们识别和记忆质数。例如:
1. 除2、3、5法:将一个数除以2、3、5后,若余数均为1,则这个数为质数。这种方法适用于初步筛选较小的质数,但需要注意的是,并非所有满足条件的数都是质数(如29除以5余4,但29仍是质数),因此还需要进一步验证。
2. 6的倍数加减1法:除了2和3以外,所有的质数都可以表示为6k±1的形式(k为自然数)。这是因为除了2和3以外,任何合数都可以被分解成两个大于1的因数的乘积,而这两个因数中至少有一个是偶数或能被3整除。由于偶数可以表示为2k(k为自然数),能被3整除的数可以表示为3k(k为自然数),因此它们的乘积可以表示为6k(k为自然数)的倍数。但是,6的倍数本身不是质数(除了6本身以外的偶数都是合数,而6的奇数倍则至少有一个因数大于1且能被3整除),所以质数只能表示为6k±1的形式。这种方法在筛选较大范围的质数时非常有用。
3. 试除法:对于一个给定的数n,我们可以用从2到√n的所有整数去除它。如果n不能被这些数整除(即余数为0),则n为质数。这种方法虽然简单直接,但当n较大时计算量会非常大。因此,在实际应用中通常会结合其他方法一起使用。
4. 筛选法:如埃拉托斯特尼筛法(Sieve of Eratosthenes)等,这些方法通过逐步排除合数来筛选出质数。这些方法在处理大量数据时非常高效。
最后需要强调的是,虽然口诀和方法可以帮助我们更好地识别和记忆质数,但要想真正掌握质数的性质和规律,还需要通过大量的练习和实践来加深理解和运用。同时,也要保持对数学的好奇心和探索精神,不断发现新的数学奥秘和乐趣。
- 上一篇: 钟字怎么写?笔顺笔画全解析
- 下一篇: 揭秘“钓鱼执法”背后的网络热梗
-
 揭秘:质数表的快速记忆口诀是什么?新闻资讯12-02
揭秘:质数表的快速记忆口诀是什么?新闻资讯12-02 -
 揭秘:轻松掌握质数的口诀!新闻资讯11-23
揭秘:轻松掌握质数的口诀!新闻资讯11-23 -
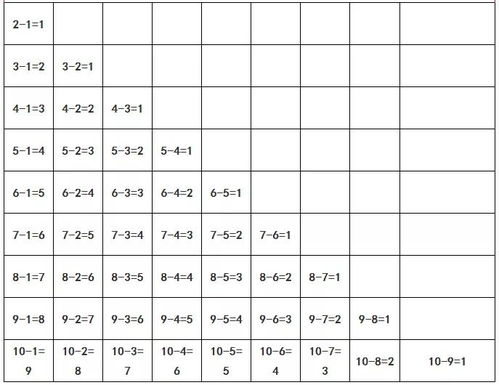 如何快速背诵加法口诀表的技巧有哪些?新闻资讯10-30
如何快速背诵加法口诀表的技巧有哪些?新闻资讯10-30 -
 掌握加法口诀表的高效背诵技巧新闻资讯10-30
掌握加法口诀表的高效背诵技巧新闻资讯10-30 -
 儿童必学:精简版小学九九乘法口诀表新闻资讯10-19
儿童必学:精简版小学九九乘法口诀表新闻资讯10-19 -
 如何有效教孩子记忆九九乘法口诀表?新闻资讯11-22
如何有效教孩子记忆九九乘法口诀表?新闻资讯11-22












