轻松掌握根号计算方法,一学就会!
根号怎么计算:探索数学中的平方根奥秘
在数学的世界里,根号(Radical)是一个既基础又充满魅力的概念,它不仅是解决许多实际问题的钥匙,也是连接代数与几何的桥梁。本文将带您深入探索根号,特别是平方根的计算方法,让您对这一数学概念有更全面、更直观的理解。

一、初识根号与平方根
首先,让我们从最基本的定义开始。根号,在数学中通常用来表示一个数的平方根。具体来说,若一个非负数$a$的平方等于$b$(即$a^2 = b$),则$a$是$b$的非负平方根。为了表示这种关系,我们使用符号$\sqrt{}$,如$\sqrt{b} = a$。特别地,当$b$为某个整数的平方时,我们可以轻松找到其精确的平方根;而当$b$不是完全平方数时,平方根则是一个无限不循环小数,即无理数。

二、手算平方根的基本方法
虽然现代科技(如计算器、电脑软件)使得计算平方根变得异常简单,但了解手算平方根的方法仍然具有教育意义,它能帮助我们更深刻地理解数的性质和运算规律。

1. 长除法(也称为牛顿法的一种简化形式):这是一种近似计算平方根的经典方法。基本思路是将被开方数分解为一系列易于处理的数字组合,然后逐步逼近真实值。例如,计算$\sqrt{252}$时,可以先估算一个接近但稍大的完全平方数(如$16^2 = 256$),然后通过逐步调整来减小误差。

2. 逐位逼近法:对于更大的数或需要更高精度的场合,可以采用逐位逼近法。这种方法通过不断尝试和调整每一位上的数字,使得计算结果的平方与被开方数越来越接近。虽然过程相对繁琐,但它是理解平方根计算原理的有效途径。
三、利用数学公式和性质
在深入学习和应用中,我们还会遇到利用数学公式和性质来计算或估计平方根的情况。
平方根的性质:如$\sqrt{ab} = \sqrt{a} \times \sqrt{b}$(当$a \geq 0$,$b \geq 0$时),这一性质可以帮助我们将复杂的平方根运算分解为更简单的部分。
平方根与完全平方数:了解常见的完全平方数(如$1^2, 2^2, 3^2, \ldots$)及其平方根,对于快速估算和验证结果非常有帮助。
二次方程与平方根:在解决二次方程(如$ax^2 + bx + c = 0$)时,经常会用到平方根来求解$x$的值。特别是当方程可以通过因式分解或配方法转化为完全平方形式时,平方根的计算就显得尤为重要。
四、计算器与软件工具的应用
随着科技的发展,计算器、智能手机上的计算器应用以及专业的数学软件(如Mathematica、MATLAB、Wolfram Alpha等)已成为计算平方根的便捷工具。这些工具不仅能快速给出准确结果,还能处理复杂的数学表达式和大规模的数据计算,极大地提高了我们的工作效率和准确性。
使用这些工具时,我们只需简单输入被开方数,按下相应的平方根按钮或输入求根函数,即可立即得到结果。同时,许多高级工具还提供了详细的计算步骤和图形展示,帮助用户更好地理解计算过程和结果。
五、平方根在日常生活中的应用
平方根不仅仅是一个抽象的数学概念,它在我们的日常生活中也有着广泛的应用。
物理学:在计算物体的速度、加速度、位移等物理量时,经常需要用到平方根。例如,根据动能公式$E_k = \frac{1}{2}mv^2$,我们可以通过已知的能量和质量来求解物体的速度。
工程学:在设计建筑、桥梁、道路等结构时,工程师需要利用平方根来计算结构的稳定性、承载能力等关键参数。
经济学:在金融领域,平方根常用于计算投资回报率的标准差等统计指标,帮助投资者评估风险。
几何学:在解决与圆、正方形、矩形等图形相关的问题时,平方根也是不可或缺的工具。例如,圆的面积和周长都与半径的平方根有关。
六、结语
通过以上的探讨,我们不难发现,根号及其背后的平方根计算不仅是一个重要的数学概念,更是连接多个学科领域和应用场景的关键纽带。无论是通过手算方法、利用数学公式和性质,还是借助现代科技工具,掌握平方根的计算方法都能为我们的学习和生活带来诸多便利。希望本文能够激发您对根号及其计算方法的进一步兴趣,并在未来的学习和实践中不断探索和应用。
- 上一篇: 苹果手机安装影音先锋播放器的简易步骤
- 下一篇: 当12345热线失效,教你如何有效投诉解决问题!
-
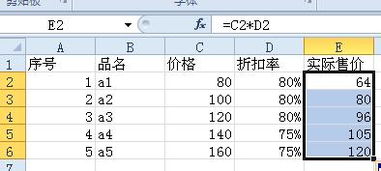 揭秘!折扣价格究竟如何计算?一学就会的省钱妙招!新闻资讯10-29
揭秘!折扣价格究竟如何计算?一学就会的省钱妙招!新闻资讯10-29 -
 [中括号「[]」究竟该怎么打?一学就会的秘诀!]新闻资讯11-13
[中括号「[]」究竟该怎么打?一学就会的秘诀!]新闻资讯11-13 -
 揭秘!圆形面积的神奇计算公式,一学就会的几何奥秘新闻资讯10-23
揭秘!圆形面积的神奇计算公式,一学就会的几何奥秘新闻资讯10-23 -
 轻松掌握:他的笔顺书写秘籍,一学就会!新闻资讯10-19
轻松掌握:他的笔顺书写秘籍,一学就会!新闻资讯10-19 -
 想知道每个汉字的'每'字笔顺?一学就会,轻松掌握正确书写方法!新闻资讯10-21
想知道每个汉字的'每'字笔顺?一学就会,轻松掌握正确书写方法!新闻资讯10-21 -
 轻松掌握:船的拼音拼读技巧,一学就会!新闻资讯10-25
轻松掌握:船的拼音拼读技巧,一学就会!新闻资讯10-25












