揭秘:六的倍数有哪些?
六的倍数是什么

六的倍数,这个数学概念听起来简单,实则蕴含着丰富的数学原理和实际应用。简单来说,六的倍数就是所有可以被6整除的整数。为了更直观地理解六的倍数,我们可以从基本的数学定义出发,逐步探讨其特性、规律以及在生活中的应用。
首先,我们需要明确什么是倍数。在数学上,倍数是指一个整数能够被另一个整数整除,不留余数。比如,2的倍数有2、4、6、8等,因为这些数都可以被2整除。同理,六的倍数就是能被6整除的整数,例如6、12、18、24等。
接下来,我们来观察六的倍数的特性。通过观察可以发现,六的倍数具有以下特点:
1. 结尾数字有规律:六的倍数的个位数通常是0、2、4、6、8。这是因为当我们将这些数除以6时,余数为0,满足倍数的定义。当然,这个规律只是帮助我们快速判断一个数是否可能是六的倍数,但并不是绝对的,因为还需要验证该数能否被6整除。
2. 每隔六个数出现一次:在自然数序列中,六的倍数每隔六个数就会出现一次。比如,6是第一个六的倍数,接着是12(6+6),然后是18(12+6),以此类推。这个规律可以帮助我们快速找到任意位置上的六的倍数。
3. 可以被其他因数整除:由于6=2×3,所以六的倍数必然可以被2和3整除。这是倍数性质的一个推广,即如果一个数是A和B的乘积的倍数,那么它也可以被A或B整除。
为了更深入地理解六的倍数,我们可以探索其内在的生成规律。从数学上讲,六的倍数可以通过将6乘以任意整数得到。这个整数可以是正数、负数或零。比如,当我们将6乘以1时,得到6;乘以2时,得到12;乘以-1时,得到-6;乘以0时,得到0。这些数都是六的倍数。
在实际应用中,六的倍数有着广泛的应用。以下是一些常见的应用场景:
1. 时间计算:在日常生活中,我们经常使用六的倍数来计算时间。比如,一个小时有60分钟,而60分钟正好是6的10倍。因此,在很多与时间相关的计算中,六的倍数都会出现。此外,一天有24小时,而24也是6的4倍。这些规律使得我们在进行时间计算时更加方便。
2. 分数简化:在分数运算中,六的倍数也扮演着重要角色。比如,当我们需要将一个分数化简为最简形式时,如果分母是6的倍数,我们可以尝试将其分解为2和3的乘积,从而更容易找到分子和分母的公约数进行化简。
3. 数组排列:在计算机科学和编程中,六的倍数也经常被用于数组排列和索引计算。比如,当我们需要在一个长度为N的数组中每隔固定距离选取一个元素时,如果固定距离是6的倍数,那么我们可以利用这个规律来快速定位需要选取的元素。
4. 几何图形:在几何学中,六的倍数也与一些特殊图形的性质有关。比如,正六边形每个内角都是120度,而120度正好是6的20倍(虽然这里涉及到的是度数与倍数的概念结合,但同样体现了六的倍数在几何中的应用)。此外,在三维空间中,正八面体的每个面都是等边三角形,而等边三角形的边长与正八面体的高之间也存在与6有关的倍数关系。
为了更深入地理解六的倍数,我们可以通过一些具体的例子来进行说明。
例子一:计算100以内六的倍数
我们需要找到所有小于100且能被6整除的整数。通过逐一尝试或利用六的倍数的规律(即每隔六个数出现一次),我们可以得到以下答案:6、12、18、24、30、36、42、48、54、60、66、72、78、84、90、96。这些数都是100以内六的倍数。
例子二:利用六的倍数进行分数化简
假设我们有一个分数18/36,需要将其化简为最简形式。我们可以观察到分母36是6的倍数,因此可以将其分解为6×6。接着,我们尝试在分子和分母中找到公约数进行化简。在这个例子中,18和36都可以被6整除,所以我们可以将分子和分母都除以6,得到最简形式1/2。
例子三:在数组中应用六的倍数
假设我们有一个长度为100的数组arr,需要每隔6个元素选取一个元素进行处理。我们可以利用六的倍数的规律来快速定位需要选取的元素。具体来说,我们可以从arr[0]开始,每次跳过5个元素(因为6-1=5),选取arr[0]、arr[6]、arr[12]、...、arr[96]这些元素进行处理。
通过以上例子,我们可以看到六的倍数在数学和实际应用中的重要作用。它不仅可以帮助我们快速进行数学计算,还可以提高我们在处理实际问题时的效率和准确性。
最后,我们需要注意的是,虽然六的倍数在数学上有着明确的定义和规律,但在实际应用中,我们还需要结合具体问题的背景和条件进行灵活运用。只有这样,我们才能充分发挥六的倍数在数学和实际问题解决中的价值。
- 上一篇: 轻松学会:盖浇饭的美味制作方法
- 下一篇: 如何撰写吸引人的兴趣爱好与特长介绍
-
 国五和国六车有哪些主要区别?新闻资讯11-11
国五和国六车有哪些主要区别?新闻资讯11-11 -
 深入理解倍数的概念新闻资讯11-23
深入理解倍数的概念新闻资讯11-23 -
 揭秘因数与倍数的奇妙世界新闻资讯11-18
揭秘因数与倍数的奇妙世界新闻资讯11-18 -
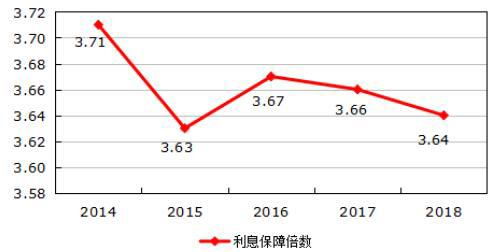 揭秘:利息保障倍数的多样性与重要性新闻资讯11-24
揭秘:利息保障倍数的多样性与重要性新闻资讯11-24 -
 如何快速求解两个数的最小公倍数?详细步骤揭秘!新闻资讯10-23
如何快速求解两个数的最小公倍数?详细步骤揭秘!新闻资讯10-23 -
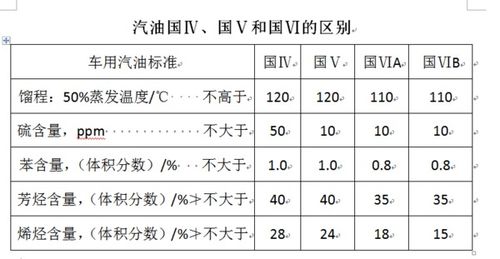 轻松掌握!国五与国六的辨别秘籍新闻资讯11-12
轻松掌握!国五与国六的辨别秘籍新闻资讯11-12












