揭秘“三线合一”的神奇内涵

“三线合一”的深入解析

在几何学中，“三线合一”是一个重要的性质，它主要出现在等腰三角形和等边三角形中。这一性质不仅揭示了三角形中某些特殊线段之间的关系，还为解决与三角形相关的问题提供了有力的工具。下面，我们将详细探讨“三线合一”的具体含义、应用以及相关的证明过程。

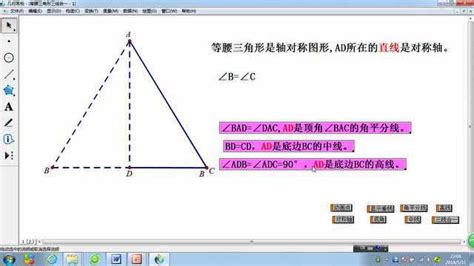
首先，我们需要明确“三线合一”中的“三线”指的是什么。在等腰三角形中，这三线分别是：底边上的中线、底边上的高线和顶角的平分线。而在等边三角形中，由于三边相等、三角相等，因此“三线合一”的性质表现得更加明显，任意一边上的中线、高线和这边所对角的平分线都是同一条线。

一、等腰三角形中的“三线合一”

在等腰三角形中，若两边相等，则它们所对的两角也相等。此时，底边上的中线、高线和顶角的平分线会重合在一起。这一性质可以通过以下步骤来证明：

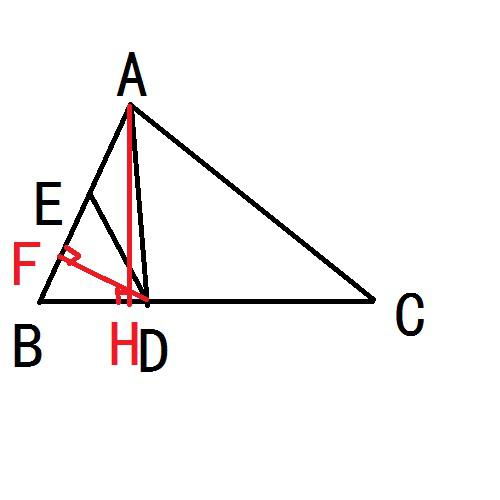
1. 设定等腰三角形：设等腰三角形为ABC，其中AB=AC，AD为BC边上的中线，AE为BC边上的高线，AF为∠BAC的平分线。

2. 利用等腰三角形的性质：由于AB=AC，根据等腰三角形的性质，我们知道∠B=∠C。

3. 证明中线与高线重合：由于AD是BC的中线，所以BD=CD。又因为AE是BC的高线，所以AE⊥BC。我们可以证明△ABD与△ACD是全等的（根据SAS全等条件），从而得出AD=AD（自反性），∠BAD=∠CAD（等腰三角形的底角相等），以及BD=CD（已知）。因此，中线AD与高线AE重合于D点。

4. 证明高线与角平分线重合：由于AE⊥BC且∠BAD=∠CAD，我们可以利用角平分线的性质来证明AE与AF重合。具体来说，由于∠BAD=∠CAD且AE是BC的高线，所以AE也是∠BAC的角平分线（即AE与AF重合）。

综上所述，我们证明了在等腰三角形中，底边上的中线、高线和顶角的平分线是重合的。

二、等边三角形中的“三线合一”

在等边三角形中，“三线合一”的性质表现得更加明显。由于等边三角形的三边相等、三角相等，因此任意一边上的中线、高线和这边所对角的平分线都是同一条线。这一性质可以通过以下步骤来证明：

1. 设定等边三角形：设等边三角形为ABC，其中AB=BC=AC，AD为BC边上的中线（同时也是高线和∠BAC的平分线）。

2. 利用等边三角形的性质：由于AB=BC=AC且∠A=∠B=∠C=60°，我们可以直接得出AD是BC的中线（因为D是BC的中点）、高线（因为AD⊥BC）和∠BAC的平分线（因为∠BAD=∠CAD=30°）。

3. 证明“三线合一”：由于AD同时满足中线、高线和角平分线的定义，因此我们可以直接得出在等边三角形中，“三线合一”的性质成立。

三、“三线合一”的应用

“三线合一”的性质在解决与三角形相关的问题时具有广泛的应用。以下是一些常见的应用场景：

1. 证明线段相等：在已知等腰三角形或等边三角形的情况下，可以利用“三线合一”的性质来证明某些线段相等。例如，在等腰三角形中，如果知道底边上的中线和高线重合，那么就可以证明底边上的两个底角所对的边（即腰）相等。

2. 证明角相等：同样地，“三线合一”也可以用来证明某些角相等。在等腰三角形中，如果知道底边上的中线和角平分线重合，那么就可以证明底边上的两个底角相等。

3. 计算角度或边长：在已知等腰三角形或等边三角形以及某些线段或角的信息的情况下，可以利用“三线合一”的性质来计算其他角度或边长。例如，在等腰三角形中，如果知道底边上的中线长度和底边长度，那么就可以利用勾股定理来计算腰的长度或顶角的度数。

4. 构造辅助线：在解决一些复杂的几何问题时，“三线合一”的性质还可以用来构造辅助线以简化问题。例如，在证明某些线段相等或角相等时，可以通过构造等腰三角形或等边三角形并利用“三线合一”的性质来简化证明过程。

四、实例分析

为了更好地理解“三线合一”的应用，我们可以举一个具体的例子进行分析：

例：已知等腰三角形ABC中，AB=AC，∠BAC=120°，D为BC的中点。求∠BAD的度数。

解：

1. 利用等腰三角形的性质：由于AB=AC，所以∠B=∠C。又因为三角形的内角和为180°，所以∠B+∠C+∠BAC=180°。将∠BAC=120°代入得∠B+∠C=60°。由于∠B=∠C，所以∠B=∠C=30°。

2. 利用“三线合一”的性质：由于D是BC的中点且AB=AC，所以AD是BC的中线也是高线（但在这个问题中我们不需要用到高线的性质）。更重要的是，AD还是∠BAC的平分线。因此，∠BAD=∠CAD=1/2∠BAC=60°。

3. 得出结论：所以∠BAD的度数为60°。

通过这个例子，我们可以看到“三线合一”的性质在解决等腰三角形相关问题时的重要作用。它不仅简化了问题的求解过程，还为我们提供了一种有效的解题思路和方法。

综上所述，“三线合一”是等腰三角形和等边三角形中一个重要的性质。它揭示了三角形中某些特殊线段之间的关系，并为解决与三角形相关的问题提供了有力的工具。通过深入理解和灵活应用这一性质，我们可以更加高效地解决各种几何问题。