充要条件的定义与解析
充要条件深度解析

充要条件是数学和逻辑学中的一个核心概念,它描述了两个命题之间的一种特定关系。理解充要条件不仅对于数学和逻辑学的深入学习至关重要,而且在日常生活和工作中也能帮助我们做出更加准确和科学的决策。本文将从充要条件的定义、性质、应用以及与充分条件和必要条件的关系等多个方面进行全面解析,以帮助读者深入理解充要条件。

一、充要条件的定义
充要条件,也称为充分必要条件,描述了两个命题之间的等价关系。具体来说,如果命题A的成立是命题B成立的充分且必要条件,即A的成立导致B的成立,且B的成立也必然导致A的成立,那么称A是B的充要条件。这可以用符号“A⇔B”来表示,读作“A当且仅当B”。

二、充要条件的性质
充要条件具有以下几个重要的性质:

1. 等价性:A是B的充要条件,意味着A与B在逻辑上是等价的,即它们要么同时为真,要么同时为假。这种等价性体现了充要条件的本质特征。
2. 对称性:如果A是B的充要条件,那么B也是A的充要条件。这反映了充要条件在逻辑上的对称性,即两个命题可以互换位置而不改变它们之间的充要关系。
3. 传递性:如果A是B的充要条件,B是C的充要条件,那么A也是C的充要条件。这一性质表明,充要条件可以沿着命题链传递下去,形成一个逻辑上的等价类。
4. 自反性:任何命题都是自身的充要条件。这意味着任何命题都与其自身等价,即它们之间既充分又必要。
三、充要条件的应用
充要条件在数学、逻辑学和其他学科中都有广泛的应用。以下是几个典型的例子:
1. 数学证明:在数学中,充要条件经常用于证明定理或推导公式。例如,在证明两个三角形全等时,可以通过证明它们的三边分别相等或者两角及夹边分别相等来实现。这里提到的两个条件就是三角形全等的充要条件。
2. 逻辑判断:在逻辑学中,充要条件可以用来判断命题的真假。如果一个命题是另一个命题的充要条件,那么它们的真假状态必须一致。这使得充要条件成为逻辑判断的重要依据。
3. 算法设计:在计算机科学中,充要条件可以用来进行算法设计和优化。通过识别问题的充要条件,可以设计出更高效、更简洁的算法来解决实际问题。
四、充要条件与充分条件和必要条件的关系
为了更全面地理解充要条件,我们需要将其与充分条件和必要条件进行比较。
1. 充分条件:如果命题A的成立是命题B成立的充分条件,那么A的成立必然导致B的成立,但B的成立不一定导致A的成立。记作“A→B”。
2. 必要条件:如果命题A的成立是命题B成立的必要条件,那么B的成立必然导致A的成立,但A的成立不一定导致B的成立。记作“B→A”。
3. 充要条件:如上文所述,A是B的充要条件意味着A的成立既充分又必要地导致B的成立,且B的成立也既充分又必要地导致A的成立。记作“A⇔B”。
可以看出,充要条件同时具备充分条件和必要条件的性质。如果A是B的充要条件,那么A也是B的充分条件和必要条件;反之亦然。
五、充要条件的实例分析
为了更好地理解充要条件的概念和性质,我们可以分析一些具体的实例:
1. 数学例子:在实数范围内,一个数x是偶数的充要条件是它可以被2整除。即,如果x是偶数,那么它可以被2整除;反之,如果x可以被2整除,那么它是偶数。这里,“x是偶数”和“x可以被2整除”是充要条件。
2. 逻辑例子:考虑两个命题:“所有S都是P”和“存在一个S不是P”。这两个命题是互相矛盾的,因此它们不能互为充要条件。但是,“所有S都是P”的充要条件是“没有一个S不是P”,而“存在一个S不是P”的充要条件是“不是所有S都是P”。这里体现了充要条件在逻辑上的等价性。
3. 生活例子:考虑一个日常生活中的例子:一个人要想成为一名合格的医生,必须接受医学教育并获得相关资质证书。同时,如果一个人已经接受了医学教育并获得了相关资质证书,那么他就有资格成为一名医生。这里,“接受医学教育并获得相关资质证书”是“成为一名合格的医生
- 上一篇: 淘宝省钱卡在哪取消自动续费?详细步骤来了!
- 下一篇: 如何设置支付宝商家二维码收款
-
 探索平衡力的奥秘:精准定义解析新闻资讯11-05
探索平衡力的奥秘:精准定义解析新闻资讯11-05 -
 解析:屌丝定义与女屌丝特质详解新闻资讯10-24
解析:屌丝定义与女屌丝特质详解新闻资讯10-24 -
 普信男与普信女的定义解析新闻资讯11-26
普信男与普信女的定义解析新闻资讯11-26 -
 人口红利定义及含义解析新闻资讯11-17
人口红利定义及含义解析新闻资讯11-17 -
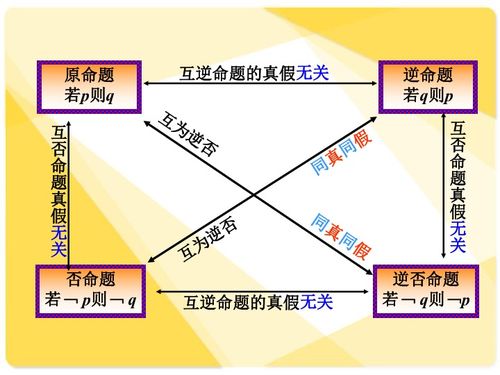 揭秘:充分条件与必要条件的奥秘与区别新闻资讯11-04
揭秘:充分条件与必要条件的奥秘与区别新闻资讯11-04 -
 not until倒装句的定义与用法新闻资讯10-30
not until倒装句的定义与用法新闻资讯10-30












