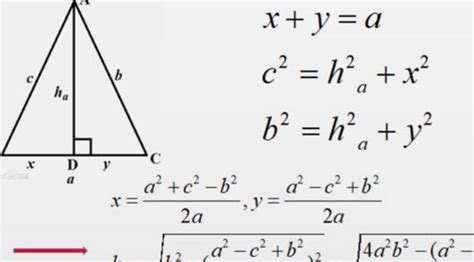揭秘:轻松计算三角形边长的神奇公式
在几何学中,三角形是最基本的形状之一,具有广泛的应用,从建筑设计到计算机图形学,再到物理学中的力学分析。为了理解和应用三角形,我们需要掌握其边长和角度之间的关系。尽管三角学涵盖了广泛的概念,但当我们聚焦于“求三角形边长公式”时,会发现它实际上涉及多种方法,这些方法依赖于三角形的类型和已知信息(如边长、角度)的不同。本文将从直角三角形的边长求解、一般三角形的边长求解以及使用向量方法求解三角形边长这三个维度进行探讨。
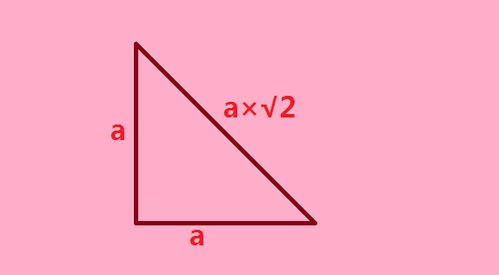
直角三角形的边长求解
直角三角形是最简单的三角形类型,因为它包含一个90度的角。在直角三角形中,三条边分别称为斜边(c)、邻边(a)和对边(b)。最著名的直角三角形边长关系由毕达哥拉斯定理给出,这个定理适用于任何直角三角形。

毕达哥拉斯定理:在直角三角形中,斜边的平方等于两直角边的平方和。数学表达式为:
c² = a² + b²
这个公式是求解直角三角形边长的基石。如果你知道其中两边的长度,就可以轻松计算出第三边的长度。例如,如果已知直角边a和b的长度,你可以通过计算a² + b²的平方根来找到斜边c的长度。
此外,对于30-60-90和45-45-90这两种特殊直角三角形,我们还可以利用它们特定的边长比例来求解边长。在30-60-90三角形中,较短的直角边是斜边的一半(即a = c/2),较长的直角边是斜边的√3/2倍(即b = c×√3/2)。在45-45-90三角形中,两直角边相等(即a = b),且斜边是直角边的√2倍(即c = a×√2 = b×√2)。
一般三角形的边长求解
对于非直角三角形,我们通常使用余弦定理和正弦定理来求解边长。
余弦定理:对于任意三角形ABC,其边长a、b、c和对应角A、B、C之间的关系可以通过余弦定理表示。对于任意一边c和对应的角C,余弦定理给出:
c² = a² + b² - 2ab·cos(C)
这个公式表明,如果我们知道三角形任意两边的长度和它们之间的夹角,就可以计算出第三边的长度。同样,也可以调整公式以解出a或b,只需将相应的边长和角度代入公式中即可。
正弦定理:正弦定理提供了另一种求解三角形边长的方法,它适用于已知两角和任意一边的情况,或者已知两边和任意一角的情况。正弦定理的表达式为:
a/sin(A) = b/sin(B) = c/sin(C)
这个公式表明,三角形的任意一边与其对应角的正弦值的比值是常数,这个常数等于其他两边与其对应角的正弦值的比值。因此,如果我们知道两个角和一条边的长度,就可以利用正弦定理求解另一条未知边的长度。
使用向量方法求解三角形边长
在现代数学和物理学中,向量提供了一种强大的工具来分析几何问题,包括三角形的边长求解。向量不仅可以表示大小和方向,还可以用来描述点在空间中的位置和运动。
在二维平面上,一个向量可以表示为(x, y)的形式,其中x和y是向量在x轴和y轴上的分量。三角形的边长可以通过计算向量之间的模(或长度)来得到。
假设三角形ABC的三个顶点分别是A(x₁, y₁)、B(x₂, y₂)和C(x₃, y₃)。则向量AB可以表示为(x₂ - x₁, y₂ - y₁),向量AC可以表示为(x₃ - x₁, y₃ - y₁)。
向量模的计算:一个向量的模(即长度)可以通过以下公式计算:
|V| = √(x² + y²)
将向量AB和AC的分量代入上述公式,即可得到AB和AC的长度,即三角形ABC的两边a和b。要找到第三边BC的长度,可以先计算向量BC(即(x₃ - x₂, y₃ - y₂)),然后同样使用模的公式计算其长度。
此外,向量还可以用来求解三角形的角度。例如,向量AB和AC之间的夹角θ可以通过向量的点积公式来计算:
cos(θ) = (AB · AC) / (|AB| × |AC|)
其中,点积AB · AC = (x₂ - x₁)(x₃ - x₁) + (y₂
- 上一篇: 手机屏幕变黑如何调回正常色彩
- 下一篇: 如何让青鱼做得更加美味?
-
 揭秘!直角三角形面积计算的神奇公式新闻资讯10-30
揭秘!直角三角形面积计算的神奇公式新闻资讯10-30 -
 揭秘!三角形面积计算的神奇等式是什么?新闻资讯10-21
揭秘!三角形面积计算的神奇等式是什么?新闻资讯10-21 -
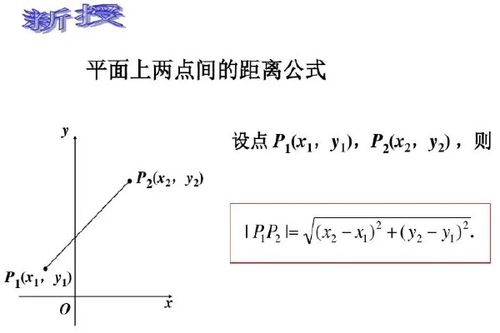 揭秘!两点间距离公式的神奇奥秘,让距离计算变得如此简单新闻资讯10-23
揭秘!两点间距离公式的神奇奥秘,让距离计算变得如此简单新闻资讯10-23 -
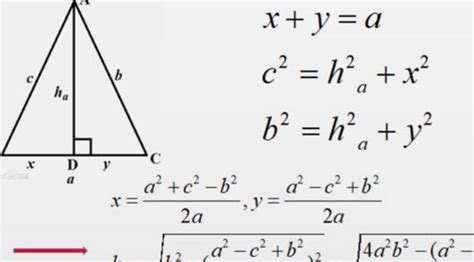 小学五年级学生如何计算三角形面积?请告知公式新闻资讯10-29
小学五年级学生如何计算三角形面积?请告知公式新闻资讯10-29 -
 等腰三角形面积公式是什么?已知腰长该如何求解?新闻资讯10-31
等腰三角形面积公式是什么?已知腰长该如何求解?新闻资讯10-31 -
 正方体表面积计算公式详解新闻资讯12-03
正方体表面积计算公式详解新闻资讯12-03