一立方计算全攻略:轻松掌握立体空间度量方法
一立方,究竟怎么算?揭秘立方体的奇妙世界

在我们生活的多维空间中,立方体作为一个基础的几何形态,承载着无数的奥秘和实用价值。你是否曾经好奇过,一立方究竟是怎么计算出来的?这个看似简单的问题,其实背后隐藏着丰富的数学知识和实际应用。今天,就让我们一起揭开立方体的神秘面纱,探索它的计算方法和在日常生活中的广泛应用。
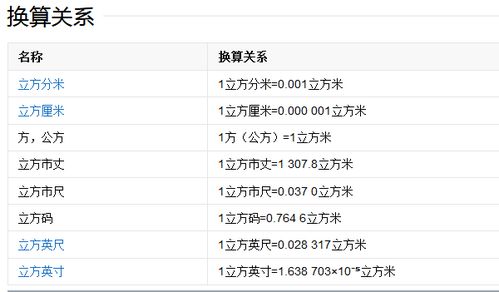
一、立方体的定义与特性
首先,我们来明确一下立方体的定义。立方体,也称为正方体,是六个面都是正方形的特殊长方体。它的每个面都是一个正方形,所有的棱长都相等。这种规则的几何形状不仅在视觉上给人带来整齐划一的美感,更在结构和功能上展现出独特的优势。
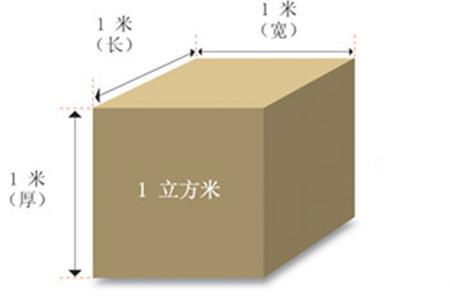
立方体的特性主要包括以下几点:
1. 六个面:每个面都是一个正方形,面积相等。
2. 十二条棱:每条棱的长度都相等,且棱与棱之间互相平行。
3. 八个顶点:每个顶点都是三条棱的交点。
二、立方体的体积计算
接下来,我们重点讨论如何计算立方体的体积。体积是三维空间中物体所占的空间大小,对于立方体来说,其体积的计算公式是:
体积 = 边长 × 边长 × 边长
或者简写为:
体积 = 边长³
这个公式看起来简单,但实际上蕴含了深刻的几何意义。它告诉我们,立方体的体积与其边长的三次方成正比。换句话说,如果立方体的边长增加一倍,其体积将增加八倍。这就是立方增长的魅力所在,也是为什么在数学和物理学中,立方体的体积计算如此重要。
三、立方体的表面积计算
除了体积之外,立方体的表面积也是一个重要的几何量。表面积是指物体外部所有面的面积之和。对于立方体来说,其表面积的计算公式是:
表面积 = 6 × (边长 × 边长)
或者简写为:
表面积 = 6 × 边长²
这个公式告诉我们,立方体的表面积与其边长的平方成正比。与体积的立方增长不同,表面积的增长是平方级的。这意味着,当立方体的边长增加一倍时,其表面积将增加四倍,而不是八倍。
四、立方体的实际应用
立方体不仅在几何学中有重要的地位,更在实际生活中有着广泛的应用。以下是几个典型的例子:
1. 建筑领域:在建筑设计中,立方体是一个常见的形状。它的规则的外观和稳定的结构使得它成为许多建筑物的首选形状。例如,一些现代的公寓楼、办公楼和仓库就采用了立方体的形式来优化设计和降低成本。
2. 储物空间:在日常生活中,我们经常会使用到各种储物箱、储物柜和集装箱等储物设备。这些设备往往采用立方体的形状来最大化存储空间。通过将物品整齐地摆放在立方体内,我们可以有效地利用空间,避免浪费。
3. 包装材料:在包装设计中,立方体也是一个常用的形状。通过将产品放置在立方体的包装盒内,可以确保产品在运输和储存过程中的安全性和稳定性。同时,立方体的形状也使得包装盒的制作和加工更加简单和高效。
4. 游戏与玩具:在游戏和玩具领域中,立方体也是一个常见的元素。例如,魔方就是一种由多个小立方体组成的智力玩具。通过旋转和移动这些小立方体,玩家可以挑战自己的思维能力和空间想象力。
五、立方体的趣味数学
除了实际应用之外,立方体还与许多有趣的数学问题紧密相关。以下是一些与立方体相关的趣味数学知识:
1. 立方和公式:在数学中,有一个著名的公式叫做立方和公式。它描述了两个立方数的和可以表示为一个立方数减去另一个立方数的形式。这个公式在代数和数论中有着广泛的应用。
2. 费马大定理:费马大定理是一个著名的数学难题,它断言对于任何大于2的整数n,方程x^n + y^n = z^n都没有正整数解。虽然这个定理的证明在1995年才由英国数学家安德鲁·怀尔斯完成,但立方体的形式(n=3)早在几千年前就被数学家们研究过。
3. 立方根与立方数:立方根是指一个数的立方等于另一个数时,这个数就是被开立方数的立方根。例如,2的立方是8,所以8的立方根是2。立方数则是指一个数的三次方。例如,3的立方是27,所以27是一个立方数。
4. 几何级数增长:立方体的体积增长是一个典型的几何级数增长过程。这种增长方式在自然界和经济学中都有广泛的应用。例如,在生物学中,细胞的分裂过程就遵循着几何级数的增长规律;在经济学中,复利计算也利用了这种增长方式来实现财富的快速增长。
六、结语
通过对立方体的深入探索,我们不仅了解了它的定义、特性和计算方法,还发现了它在日常生活中的广泛应用和趣味数学知识。
- 上一篇: 创意折纸大揭秘:轻松打造立体五角星,手工DIY教程
- 下一篇: 轻松掌握:支付宝账号注册全步骤指南
-
 揭秘:如何轻松计算一立方体积?新闻资讯11-25
揭秘:如何轻松计算一立方体积?新闻资讯11-25 -
 揭秘!立方米与升之间的轻松换算秘籍,让单位转换不再困扰新闻资讯10-23
揭秘!立方米与升之间的轻松换算秘籍,让单位转换不再困扰新闻资讯10-23 -
 如何计算一立方体积新闻资讯11-08
如何计算一立方体积新闻资讯11-08 -
 一立方水究竟有多重?答案揭晓:等于多少吨?新闻资讯11-14
一立方水究竟有多重?答案揭晓:等于多少吨?新闻资讯11-14 -
 揭秘!立方米与立方厘米之间的神奇转换率,让度量不再迷茫新闻资讯10-28
揭秘!立方米与立方厘米之间的神奇转换率,让度量不再迷茫新闻资讯10-28 -
 真空度计算公式详解,轻松掌握计算方法!新闻资讯11-12
真空度计算公式详解,轻松掌握计算方法!新闻资讯11-12










