自然数的定义及详解
在数学的浩瀚宇宙中,有一类数字如同夜空中最璀璨的星辰,它们简单、直观,却又蕴含着无尽的奥秘与力量,这便是自然数。对于初次踏入数学殿堂的你,或许正怀揣着对“什么是自然数”的好奇与探索欲。那么,让我们一同踏上这场关于自然数的奇妙之旅,揭开它神秘的面纱。
自然数的起源与定义
追溯至远古时代,当人类祖先开始计数猎物、分配食物时,自然数的概念便悄然萌芽。最初,它们可能是以手指、石子或刻痕等形式出现,用以表示数量的多少。随着文明的进步,这些原始计数方式逐渐演变为更加抽象、系统的数字体系,自然数便是这一体系中的基石。
简而言之,自然数是从0开始,依次递增的正整数序列,即0、1、2、3、4……每一个自然数都代表了一个确定的量,且每一个数都比前一个数大1。在数学中,自然数集通常用符号N(有时也包括0,有时则不包含,这取决于具体的数学定义和上下文)来表示。
自然数的性质与特征
自然数不仅仅是一串简单的数字,它们还拥有着独特的性质与特征,这些性质构成了数学推理与证明的基础。
1. 无限性:自然数是无限的,无论我们数到多大的数字,总有一个更大的自然数紧随其后。这种无限性使得自然数成为描述无穷大与无穷小概念的基石。
2. 有序性:自然数按照从小到大的顺序排列,每个数都有一个确定的位置,且每个位置上的数都是唯一的。这种有序性为比较大小、排序等操作提供了可能。
3. 封闭性:在自然数集内进行加法、减法(仅限于足够大的减数)、乘法运算时,结果仍属于自然数集。这一性质保证了自然数在运算中的稳定性和自洽性。
4. 传递性:如果a小于b,b小于c,那么a必然小于c。这种传递性关系使得自然数之间形成了严格的等级结构。
5. 可加性:任意两个自然数相加,其结果仍为自然数。这一性质是自然数在计数、测量等实际应用中不可或缺的基础。
自然数的应用与意义
自然数不仅仅是数学课本上的抽象概念,它们在生活中无处不在,扮演着至关重要的角色。
计数工具:在日常生活中,我们无时无刻不在使用自然数进行计数,无论是数钱、数人数,还是计算时间、距离等,自然数都是不可或缺的计数工具。
逻辑推理:自然数的有序性和封闭性为逻辑推理提供了坚实的基础。在数学证明中,我们常常利用自然数的性质来构建证明过程,确保结论的正确性。
编码与存储:在计算机科学中,自然数被广泛应用于数据的编码与存储。无论是文本、图像还是音频文件,都可以通过一系列的自然数来表示和存储。
物理学与工程学:在物理学和工程学中,自然数常被用来描述物理量的离散变化,如粒子的数量、电路的开关状态等。此外,自然数在描述空间结构、时间序列等方面也发挥着重要作用。
自然数与数学之美
自然数不仅仅是实用的工具,它们还蕴含着数学之美。在数学的世界里,自然数以其简洁、对称、和谐的形式展现着宇宙的秩序与规律。
素数之谜:素数,即只能被1和自身整除的自然数,如2、3、5、7等。尽管素数在自然数中只占极少数,但它们的分布却遵循着神秘的规律——素数定理。素数的研究不仅推动了数学的发展,还涉及到了密码学、计算机科学等多个领域。
斐波那契数列:斐波那契数列是一组由0和1开始,后续每一项都是前两项之和的自然数序列,即0、1、1、2、3、5、8……这个数列在自然界中无处不在,如松果的鳞片排列、向日葵的花瓣分布等,都遵循着斐波那契数列的规律。斐波那契数列不仅展现了自然数的和谐之美,还揭示了自然界中普遍存在的数学规律。
黄金比例:黄金比例,即(√5-1)/2,是一个与自然数密切相关的无理数。它代表了自然界中最美的比例关系,广泛应用于建筑、艺术、音乐等领域。黄金比例的存在证明了自然数与美学之间的紧密联系。
自然数的未来探索
随着科技的进步和数学的发展,自然数的研究也在不断深化和拓展。在数学领域,自然数仍然是数论、组合数学等分支学科的研究重点。而在计算机科学中,随着大数据、人工智能等技术的兴起,自然数在数据处理、算法设计等方面的应用将更加广泛。
此外,随着人类对宇宙的认知不断深入,自然数在描述宇宙结构、探索宇宙规律方面的作用也将日益凸显。未来,我们或许能够借助自然数的力量,解开更多
-
 SEO详解:你不可不知的SEO定义及SEOer的角色关系新闻资讯11-28
SEO详解:你不可不知的SEO定义及SEOer的角色关系新闻资讯11-28 -
 Ln(自然对数)的定义与公式详解新闻资讯10-29
Ln(自然对数)的定义与公式详解新闻资讯10-29 -
 KOL定义及含义详解新闻资讯10-22
KOL定义及含义详解新闻资讯10-22 -
 摆渡车定义及用途详解新闻资讯11-07
摆渡车定义及用途详解新闻资讯11-07 -
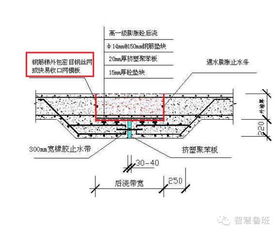 后浇带定义及施工步骤详解新闻资讯11-10
后浇带定义及施工步骤详解新闻资讯11-10 -
 详解CDR软件:定义、功能及应用解析新闻资讯10-24
详解CDR软件:定义、功能及应用解析新闻资讯10-24







