揭秘:不等式的性质全解析
不等式是数学中一个重要的概念,它描述了两个量之间的大小关系。在不等式的研究中,有一系列基本性质和定理,它们为我们解决不等式问题提供了有力的工具。以下是关于不等式性质的一些详细探讨:

不等式的性质主要分为基本性质、运算性质、取反性质、取绝对值性质、平方性质、乘除正负数性质、传递性以及可加性与可乘性等多个方面。
首先,我们来看不等式的基本性质。基本性质中包括了对称性、加法性质、乘法性质、数乘性质以及同向不等式可加性。对称性指的是,如果a>b,那么bb,c>d,那么a+c>b+d;乘法性质则是,如果a>b,c>0,那么ac>bc;数乘性质是指,如果a>b,k是正数,那么ka>kb;同向不等式可加性表明,如果a>b,c>d,那么a+d>b+c不一定成立,但a+b>c+d(同向可加),a+c>b+d(同向可加)。
接下来是不等式的运算性质。这些性质涵盖了不等式的加减乘除运算。不等式的加减运算需要注意,当两边同时加上(或减去)同一个数(或式子)时,不等号的方向不变。例如,如果a>b,那么a+c>b+c,a-c>b-c。不等式的乘法运算稍显复杂,当两边同时乘以(或除以)同一个正数时,不等号的方向同样不变;但当两边同时乘以(或除以)同一个负数时,不等号的方向会发生改变。例如,如果a>b,c>0,那么ac>bc,a/c>b/c;但如果d<0,那么adb/d。
不等式的取反性质也是一个重要的性质。它表明,如果a>b,那么-a<-b。这个性质在处理含有负号的不等式时非常有用。
取绝对值性质则涉及到不等式两边的绝对值。它指出,如果|a|>|b|,那么a²>b²;如果a>b>0,那么a的n次方>b的n次方(n是正整数);如果a>b,那么1/a<1/b(b≠0);如果a>b>0,那么a的n次方根>b的n次方根(n为奇数)。这些性质在处理含有绝对值或幂运算的不等式时非常有帮助。
平方性质指出,如果a>b>0或ab²。这个性质在判断两个数的平方大小时非常实用。
乘除正负数性质进一步强调了乘法运算中正负数的影响。它指出,当不等式两边同号时,不等式两边同时乘以一个负数,不等号方向改变;当不等式两边异号时,不等式两边同时乘以一个负数,不等号方向不改变。同时,不等式两边同号时,不等式两边同除以一个正数,不等号方向不变;不等式两边异号时,不等式两边同除以一个负数,不等号方向改变。
不等式的传递性是一个非常重要的性质,它表明如果a>b且b>c,那么a>c。这个性质在证明不等式链时非常有用。
此外,不等式还具有可加性与可乘性。可加性指的是,如果a>b,c>d,那么a+c与b+d的大小关系无法确定,但a+b>b+a=c+a>c+b,即a+b>c+d(同向不等式可加性);同时,a+(-b)>c+(-d),即a-b>c-d。可乘性则表明,如果a>b>0,c>d>0,那么ac>bd;如果a>b且c>d,那么a与c,b与d的大小关系无法确定,但是a×d与b×c的大小关系也无法确定。不过,当a、b、c、d均为正数时,可乘性可以简化为:如果a>b且c>d,那么ac>bd。
在利用不等式性质解题时,我们还需要注意一些常见的错误。例如,在运用乘法性质时,容易忽视“负数乘不等式要变号”的原则;在运用加法性质时,也容易忽视“不等式两边同时加上(或减去)同一个数(或式子),不等号的方向不变”的前提。此外,对于含有多个变量和复杂运算的不等式问题,我们还需要灵活运用各种性质和定理进行推导和求解。
在实际应用中,不等式性质具有广泛的用途。在物理、化学、经济等领域中,不等式常常用来描述各种实际问题的数量关系和变化规律。
-
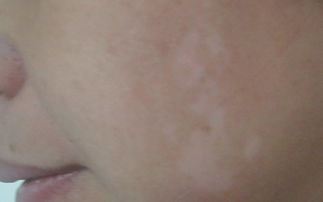 揭秘白斑真相:不同类型白斑全解析新闻资讯11-05
揭秘白斑真相:不同类型白斑全解析新闻资讯11-05 -
 揭秘:掌握数学精髓,三个不可或缺的中值定理公式详解新闻资讯11-08
揭秘:掌握数学精髓,三个不可或缺的中值定理公式详解新闻资讯11-08 -
 心肌梗塞的典型预警症状全解析!新闻资讯10-18
心肌梗塞的典型预警症状全解析!新闻资讯10-18 -
 韩式新娘优雅盘发全步骤揭秘新闻资讯06-22
韩式新娘优雅盘发全步骤揭秘新闻资讯06-22 -
 如何求解一元二次不等式?新闻资讯11-14
如何求解一元二次不等式?新闻资讯11-14 -
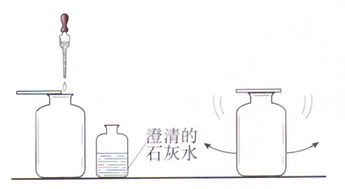 揭秘:澄清石灰水的神奇功效与应用新闻资讯11-26
揭秘:澄清石灰水的神奇功效与应用新闻资讯11-26












