揭秘!圆的周长计算方法,轻松掌握不求人
在探讨数学世界中一个基础而又至关重要的概念时,我们不可避免地会聚焦于“圆的周长”这一话题。圆的周长,即我们通常所说的圆的边界线长度,是几何学里一个既古老又常新的课题。它不仅在日常生活中有着广泛的应用,如轮胎的周长影响车辆的行驶距离,还是理解更高深数学原理,如微积分学的起点之一。那么,如何准确地计算出圆的周长呢?以下,我们将一步步深入解析这一问题的核心。
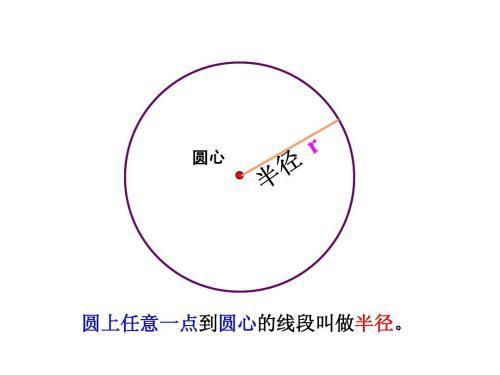
一、圆的定义与基本属性
首先,让我们从圆的定义开始。圆是平面上所有与给定点(称为圆心)距离相等的点的集合,这个相等的距离被称为圆的半径,记作r。有了这个基础,我们可以进一步探讨圆的一些基本属性,其中最为人所熟知的便是“圆的周长”或“圆的边界线长度”。
二、圆周率的引入
在计算圆的周长时,一个至关重要的常数浮现出来——圆周率π(Pi)。圆周率是一个无理数,其值约为3.14159...,表示的是圆的周长与其直径之比。这个比例对于所有圆都是相同的,不依赖于圆的大小,这一性质使得圆周率的发现和应用成为了数学史上的一个重要里程碑。
三、圆的周长计算公式
基于圆周率的定义,我们可以推导出计算圆的周长的公式:C = 2πr,其中C代表圆的周长,r是圆的半径。这个公式简洁而有力,它告诉我们,只要知道圆的半径,就可以通过乘以2π来求得圆的周长。同样地,如果我们知道圆的直径(即半径的两倍),也可以利用公式C = πd(d为直径)来计算。
四、公式的应用实例
为了更直观地理解如何应用这个公式,我们可以看几个具体的例子:
1. 假设我们有一个半径为5厘米的圆:
使用公式C = 2πr,代入r = 5厘米,得到C = 2 * π * 5 ≈ 2 * 3.14 * 5 = 31.4厘米。
因此,这个圆的周长约为31.4厘米。
2. 再来看一个直径为10米的圆:
使用公式C = πd,代入d = 10米,得到C = π * 10 ≈ 3.14 * 10 = 31.4米。
结果与上一个例子相同,因为直径是半径的两倍,所以无论使用哪个公式,结果都是一致的。
五、圆周率的历史与探索
圆周率π的精确值自古以来就是数学家们追求的目标。从古代埃及人、巴比伦人的粗略估算,到古希腊数学家阿基米德(Archimedes)的“穷竭法”,再到中国南北朝时期的数学家祖冲之将π计算到小数点后七位,人类对π的认识不断深化。如今,随着计算机技术的飞速发展,π的值已经被计算到了数十万亿位,但其真正的本质仍然吸引着无数数学家和爱好者的好奇心。
六、圆周长的实际应用
圆的周长计算不仅仅停留在理论层面,它在现实生活中有着广泛的应用。从建筑工程中的圆形结构设计,到物理学中的波动与振动分析,再到航空航天领域的精确计算,都离不开对圆周长的准确理解和应用。特别是在工程设计和制造中,精确计算圆的周长对于确保产品的质量和性能至关重要。
七、结语
综上所述,圆的周长计算是数学中一个基础而重要的知识点。通过掌握圆周率的定义和圆的周长计算公式,我们可以轻松地求解出任何圆的周长。同时,这一过程也让我们深刻体会到数学与现实生活的紧密联系以及数学在推动人类社会发展中的重要作用。在未来的学习和探索中,让我们继续保持对数学的热爱和好奇心,不断挖掘数学世界的奥秘和魅力。
-
 揭秘!轻松掌握圆的周长计算方法,让数学不再绕圈圈新闻资讯10-28
揭秘!轻松掌握圆的周长计算方法,让数学不再绕圈圈新闻资讯10-28 -
 揭秘!圆的周长计算公式大公开,你也能轻松算出来!新闻资讯10-28
揭秘!圆的周长计算公式大公开,你也能轻松算出来!新闻资讯10-28 -
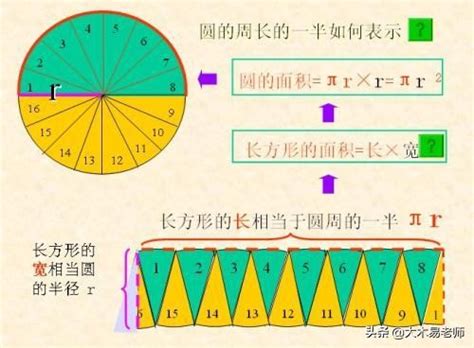 如何计算圆的周长?新闻资讯10-28
如何计算圆的周长?新闻资讯10-28 -
 如何计算扇形的周长新闻资讯11-06
如何计算扇形的周长新闻资讯11-06 -
 揭秘!圆形面积计算公式的奥秘,轻松掌握不再难新闻资讯10-19
揭秘!圆形面积计算公式的奥秘,轻松掌握不再难新闻资讯10-19 -
 Pi Values from 1 to 7新闻资讯12-11
Pi Values from 1 to 7新闻资讯12-11










